Calculer des probabilités
Une des raisons majeures justifiant l'introduction d'un cours de R dans un cursus statistique est évidemment les possibilités que le langage offre dans ce domaine. Outre qu'il est extensible, comme on l'a vu plus haut, le langage R définit toute une série de fonctions statistiques directement utilisables avec la version de base. Nous commencerons l'étude de ces possibilités via les fonctions utiles aux calculs de probabilités. Les fonctions que nous allons étudier dans ce cadre ont un format similaire:
La première lettre du nom de la fonction définit ce que retourne la fonction: la probabilité associée à la valeur x de la variable aléatoire X fournie comme argument si la lettre est 'd' (soit, Proba(X=x)), la probabilité cumulée associée à cette valeur de la variable aléatoire si la lettre fournie est 'p' (soit, Proba(X≤x)), la valeur v de la variable aléatoire V correspondant à la probabilité P fournie en argument si la lettre est 'q' (soit, Proba(V≤v)=P), et des valeurs tirées au hasard selon la distribution si la première lettre est 'r'. Le reste du nom de la fonction, <distribution>, correspond aux distributions disponibles dans le langage (binom, pois, norm,...). Nous allons illustrer par des exemples de ces fonctions associés aux distributions principales rencontrées dans le cours de statistique.
I. Distribution uniforme
La distribution uniforme est une distribution pour laquelle chaque valeur de la variable aléatoire X est équiprobable. Il existe des distribution uniformes discrètes (chaque valeur de la variable aléatoire est équiprobable) et continues (chaque plage de valeurs de même largeur est équiprobable). La distribution fournie par R est une distribution continue, qui par défaut est définie entre 0 et 1. Graphiquement, la distribution correspond à une droite horizontale Y = 1 quand X varie entre 0 et 1, et Y = 0 partout ailleurs. On peut illustrer cet aspect avec la fonction 'dunif':
dunif(0.4)## [1] 1dunif(0.7)## [1] 1dunif(1.2)## [1] 0dunif(-2.1)## [1] 0dunif(1.6, min=0, max=2)## [1] 0.5Le dernier exemple illustre que si on définit la distribution entre 0 et 2 plutôt qu'entre 0 et 1, la droite horizontale est cette fois Y = 0.5 pour X entre 0 et 2, et Y = 0 ailleurs, puisque la surface totale sous la courbe correspondant à une distribution doit toujours valoir 1. Les calculs de probabilités, dans ce cas, sont évidemment très simples. Si, par exemple, on souhaite savoir la probabilité que x soit compris entre 4 et 7 quand X est une variable uniforme définie entre 2 et 10, on écrit:
punif(7,min=2,max=10)-punif(4,min=2,max=10)## [1] 0.375Un résultat qui était facilement calculable sans aide informatique. Pour illustrer l'utilisation du tirage aléatoire dans cette distribution, nous allons simuler le jet d'un dé. La valeur de la variable aléatoire est la valeur qui apparait sur la face supérieure du dé. Clairement, on peut représenter ce jet via une variable aléatoire uniforme discrète avec des valeurs possibles qui sont 1, 2, 3, 4, 5 ou 6. La manière utilisée pour générer des valeurs aléatoires correspondant à ce type de variables est le suivant:
- On tire un nombre au hasard dans une distribution continue uniforme s'étendant entre 0 et 6.
- On prend la partie entière de ce nombre, ce qui donne une valeur qui est 0, 1, 2, 3, 4 ou 5.
- On ajoute 1 au résultat, et on obtient le type de valeurs demandées.
des<-floor(runif(1000,min=0,max=6))+1
hist(des,breaks=seq(0.5,6.5,by=1.0))Quelques précisions s'imposent sur ce code. La fonction 'floor(x)' associe à la valeur x l'entier qui lui est immédiatement inférieur. En d'autres mots, ell arrondit le nombre en supprimant la virgule et les chiffres qui la suivent. Ainsi, floor(1.4) = 1 et floor(1.99) = 1. La fonction 'round', fait quant à elle un arrondi au sens habituel du terme: round(1.4) = 1 et round(1.99) = 2. Signalons qu'il existe également une fonction 'ceiling' qui fait des arrondis supérieurs, si bien que ceiling(1.4) = ceiling(1.99) = 2. La fonction 'hist' crée un histogramme, les limites des classes à représenter étant définies via l'option 'breaks'. Le résultat est affiché sur le graphique qui suit:
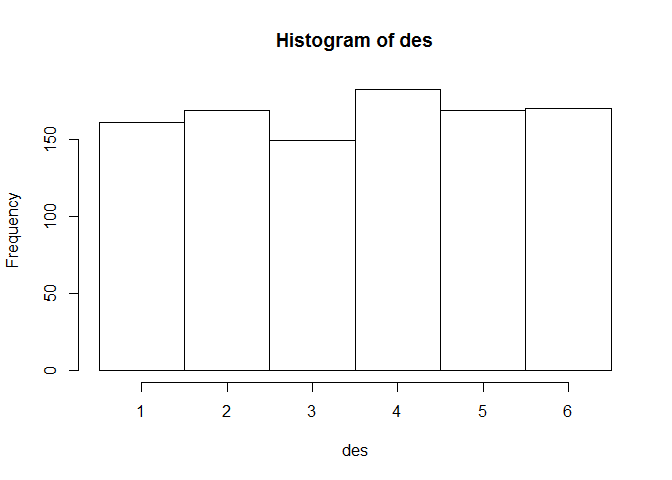
II. Distribution binomiale
Le calcul de probabilités binomiales peut se faire à partir de deux fonctions de R:
- La fonction 'dbinom(x,size=n,prob=p)' pour le calcul de la probabilité d'obtenir x fois un évènement lors de n tirages binomiaux de probabilité individuelle p (probabilité simple)
- La fonction 'pbinom(x,size=n,prob=p)' pour le calcul de la probabilité d'obtenir de 0 à x fois un évènement lors de n tirages binomiaux de probabilité individuelle p (probabilité cumulée)
Voici un exemple de code qui va illustrer l'utilisation de ces fonctionnalités: supposons qu'on recherche un variant génétique qui a une fréquence de p = 0.2 dans la population. On échantillonne n = 100 personnes, et on se demande à combien d'individus porteurs on doit s'attendre. Assez clairement, on attend en moyenne 20, soit n*p, porteurs. Bien entendu, un échantillon particulier de 100 individus ne comptera pas systématiquement 20 porteurs, le nombre r de porteurs va varier en accord avec la distribution binomiale ayant pour paramètres n et p. On pourrait également chercher entre quelles limites r a 95 % de chance de se situer. Pour répondre, on recherchera les valeur de r pour lesquelles la distribution cumulée atteint 2.5 % et 97.5 % comme suit:
p<-0.2
n<-100
for(r in 0:(n-1)){
if((pbinom(r,size=n,prob=p)<= 0.025)&& (pbinom(r+1,size=n,prob=p)>=0.025))
{low_r<-r+1}
if((pbinom(r,size=n,prob=p)<= 0.975)&& (pbinom(r+1,size=n,prob=p)>=0.975))
{high_r<-r+1}
}
low_r## [1] 12high_r## [1] 28pbinom(high_r,size=n,prob=p)-pbinom(low_r,size=n,prob=p)## [1] 0.954651Il a donc 95 % de chance d'avoir entre 12 et 28 porteurs dans cet échantillon. Une manière plus simple d'arriver à ce résultat est d'employer la fonction 'qbinom(proba,size=n,prob=p)' qui fonctionne de manière inverse à 'rbinom': on lui donne une probabilité (cumulée) en argument, et la fonction retourne la valeur de r correspondante. Le code devient donc avec cette fonction:
low_r<-qbinom(0.025,size=n,prob=p)
low_r## [1] 12high_r<-qbinom(0.975,size=n,prob=p)
high_r## [1] 28pbinom(high_r,size=n,prob=p)-pbinom(low_r,size=n,prob=p)## [1] 0.954651On peut également faire une représentation graphique de cette distribution cumulée et de ces limites avec le code suivant:
r<-0:100
pr<-pbinom(r,size=n,prob=p)
plot(r,pr)
oldpar<-par()
par(fg="blue")
abline(h=0.025)
abline(h=0.975)
par(fg="red")
abline(v=12)
abline(v=28)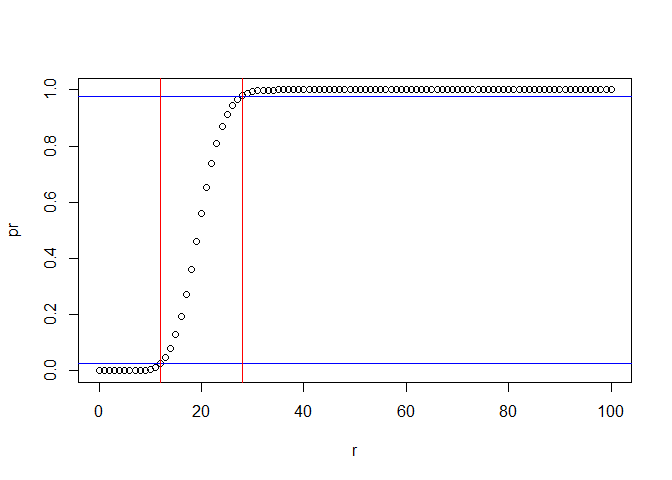
par(oldpar)Comme dernier exemple d'utilisation des fonctions liées à la distribution binomiale, on pourrait obtenir le résultat de 1000 expériences binomiales portant sur des échantillons de taille n = 100, avec une probabilité de succès à chaque tirage de p = 0.20. Cette situation correspondrait par exemple à une expérience dans laquelle 1000 poulaillers sont visités, et dans chaque poulailler, 100 poules sont testées pour la présence d'un parasite ayant une prévalence de 20 % dans la population. Chaque poulailler présentera donc entre 0 et 100 poules atteintes, et on représente le résultat de l'expérience sous la forme d'un histogramme montrant les fréquences associées aux différents cas (nombre de poules atteintes) possibles. Le code ressemblerait à ceci:
b<-seq(0.5,99.5,by=1.0)
nb_poules<-rbinom(1000,size=100,prob=0.2)
hist(nb_poules,breaks=b)Comme expliqué plus haut, la fonction 'hist' génère un histogramme, et l'option 'breaks' permet de délimiter les classes à considérer pour créer le graphique. Le graphique qui est généré est montré ci-dessous:
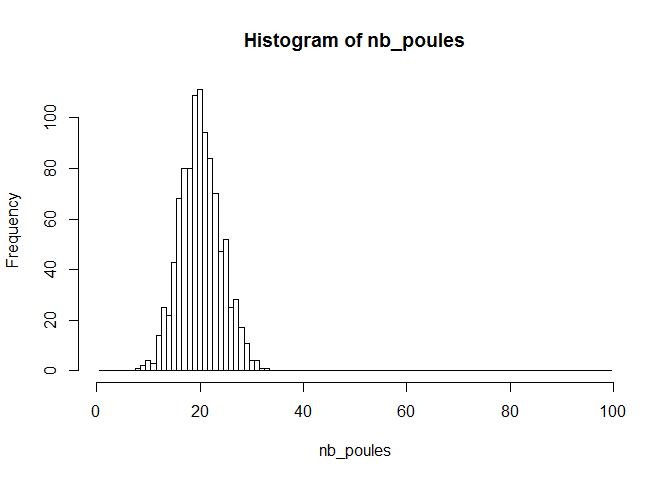
III. Distribution hypergéométrique
Dans les situations où les tirages se font sans remise, la probabilité varie à chaque tirage. On emploie alors la distribution hypergéométrique plutôt que la distribution binomiale. Illustrons la différence entre les deux distributions sur l'exemple suivant: dans un lot de 50 hamburgers, 10 sont contaminés par une salmonelle (une bactérie pathogène). Si on échantillonne au hasard 10 hamburgers dans ce lot, quelle est la probabilité de détecter la contamination ?
Tout d'abord, il est clair que la contamination sera détectée à partir du moment où au moins 1 des hamburgers testés est contaminé. Autrement dit, la seule situation dans laquelle la contamination n'est pas constatée est celle où 0 des 10 hamburgers testés n'est porteur. La probabilité de détection est donc égale à (1 - Pr(0)), où Pr(0) désigne la probabilité d'avoir 0 hamburger contaminé dans l'échantillon. Evaluons cette probabilité avec la loi binomiale pour commencer. Dans ce cas, on suppose que chacun des 10 hamburgers est testé séquentiellement, puis remis dans le lot (au risque d'être échantillonné à nouveau...). il est clair qu'en pratique, on ne procéderait pas de cette manière, mais nous le faisons ici pour illustrer la différence entre les résultats binomiaux et hypergéométriques. Le calcul pourrait se faire comme suit:
n<-10 # Nombre de hamburgers testés
p<-10/50 # Probabilité de contamination à chaque essai
Pr0<-pbinom(0,size=n,prob=p)
1-Pr0## [1] 0.8926258Venons en à présent au calcul plus réaliste, c'est-à-dire sans remise. On peut faire le calcul explicitement ou via la loi hypergéométrique. Explicitement, la probabilité d'avoir 0 hamburger contaminé dans l'échantillon de 10 correspond à la probabilité que le premier échantillon soit indemne (Proba = 40/50), puis que le second le soit aussi (Proba = 39/49), puis le troisième ... puis le dizième (Proba = 31/41). On peut donc calculer la probabilité en faisant le produit de ces probabilités, par exemple de la manière suivante:
Pr0<-1 # Initialisation
for (i in 40:31){ Pr0<-Pr0*i/(i+10)}
1-Pr0## [1] 0.9174808Une manière plus simple (?) est de faire appel à la distribution hypergéométrique:
1-dhyper(0,10,40,10)## [1] 0.9174808La principale difficulté réside dans l'interprétation des paramètres: le premier paramètre (0) est le nombre de hamburgers contaminés dans l'échantillon prélevé, le second (10) est le nombre de hamburgers contaminés dans le lot, le troisième (40) est le nombre de hamburgers non contaminés dans le lot, et le quatrième (10) est la taille de l'échantillon prélevé. On pourrait, également pour cet exemple, obtenir toute la distribution en faisant varier le premier paramètre de 0 à 10, ce qui pourrait aider à comparer avec la distribution qu'on obtiendrait si on utilisait la distribution binomiale. Le code est le suivant:
r<-0:10
prhyper<-dhyper(r,10,40,10)
prbin<-dbinom(r,size=10, prob=10/50)
plot(r, prhyper,type="o", col="red",pch=16, ylab="proba")
lines(r,prbin,col="green")
points(r,prbin,col="green",pch=16)
legend(x="topright", legend=c("hypergéométrique","binomiale"), col=c("red","green"), pch=16,lwd=1)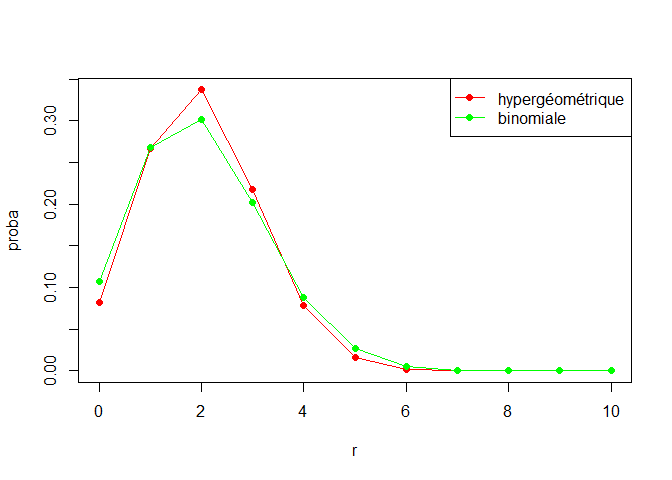
IV. Distribution de Poisson
Nous allons illustrer l'utilisation de cette distribution avec deux exemples, le premier théorique et le suivant donnant un exemple plus vétérinaire. Commençons donc par le calcul théorique. La (vraie) moyenne d'une distribution s'obtient en calculant l'espérance mathématique de la variable aléatoire, définie comme la somme sur toutes les valeurs x de la variable X du produit x*f(x), où f(x) est la valeur de la distribution en X = x. Supposons qu'on souhaite calculer la moyenne d'une distribution de Poisson, f(x) = exp(-λ)*(λ**x)/x!, où λ est un paramètre que nous prenons, par exemple, égal à 5. X est la variable aléatoire (discrète) pouvant varier de 0 à l'infini. Comme il est impossible d'effectuer le calcul explicitement (il y a une infinité de termes), nous allons montrer ce qui se passe pour les 30 premiers termes (c'est-à-dire quand x va de 0 à 29). Le code est le suivant:
esp<-0
res<-vector(mode="numeric",length=30)
val<-vector(mode="numeric", length=30)
for (x in 0:29){
esp<-esp+x*dpois(x,lambda=5)
val[x+1]<-x
res[x+1]<-esp
}
res## [1] 0.00000000 0.03368973 0.20213841 0.62326010 1.32512958 2.20246643
## [7] 3.07980327 3.81091731 4.33314163 4.65953183 4.84085971 4.93152366
## [13] 4.97273454 4.98990574 4.99651005 4.99886873 4.99965496 4.99990065
## [19] 4.99997292 4.99999299 4.99999827 4.99999959 4.99999991 4.99999998
## [25] 5.00000000 5.00000000 5.00000000 5.00000000 5.00000000 5.00000000Il est assez clair que l'espérance mathématique tend vers μ = 5 = λ, comme annoncé dans la théorie. Passons à un exemple plus vétérinaire. En Europe, en 2004, le nombre de cas de BSE était d'en moyenne 3 cas par semaine. Si on suppose que le nombre varie peu en fonction de la période de l'année, on peut simuler une année qui correspondrait à cette situation en générant 52 nombres hebdomadaires de malades au hasard à l'aide d'une distribution de Poisson de moyenne μ = λ = 3. Le code est très simple et est le suivant:
bse<-vector(mode="numeric", length=52)
bse<-rpois(52,lambda=3)
mean(bse)## [1] 3.019231La dernière instruction permet de calculer la moyenne de l'échantillon de 52 valeurs, qui s'avère dans cet exemple légèrement supérieure à la vraie moyenne.
V. Distribution de χ²
Une utilité, parmi d'autres, de la distribution de χ² est de comparer des effectifs observés à ceux qui étaient attendus sous l'hypothèse émise (appelée 'hypothèse nulle'). Par exemple, si on part de l'hypothèse qu'un facteur particulier n'a aucune incidence sur l'apparition d'une maladie, les prévalences chez les sujets exposés et chez ceux qui ne le sont pas devraient être identiques. Pour tester si l'hypothèse est raisonnable, au vu des données, la démarche est de calculer l'écart entre ce qui était prédit et ce qui est effectivement observé: si cet écart est important, on doutera de l'hypothèse. Dans le cas contraire, on lui fera confiance. La distribution de χ² permet de quantifier le mot 'important' en associant à l'écart mesuré une probabilité, qui est la probabilité d'obtenir une différence supérieure ou égale à celle effectivement observée quand l'hypothèse nulle est vraie. On peut illustrer le calcul avec un exemple (artificiel) de la manière suivante. Supposons que les données rassemblées dans une expérience sont les suivantes:
| Observations expérimentales | |||
|---|---|---|---|
| Exposés | Non exposés | Total | |
| Malades | 25 | 20 | 45 |
| Sains | 75 | 80 | 155 |
| Total | 100 | 100 | 200 |
La prévalence, mesurée sur cet échantillon est 45/200, soit 22.5 %. Si l'hypothèse d'inocuité du facteur est vraie, on s'attendrait donc à avoir 22.5 % de cas chez les exposés et 22.5 % de cas chez les non-exposés, ce qui conduirait au tableau suivant:
| Effectifs attendus sous H0 | |||
|---|---|---|---|
| Exposés | Non exposés | Total | |
| Malades | 22.5 | 22.5 | 45 |
| Sains | 77.5 | 77.5 | 155 |
| Total | 100 | 100 | 200 |
L'écart entre ce qui est attendu et observé est donc de +/- 2.5 individus. Il est expliqué dans le cours de statistiques qu'une mesure synthétique de l'écart entre attendus et observés, intégrant toutes les catégories de la table et tenant compte de l'effectif de chaque situation (un écart de 2.5 individus sur un total de 5 individus est plus important qu'un écart de 2.5 individus sur 1000 individus) est la somme des écarts élevés au carré et divisés par l'effectif attendu. Dans notre exemple, on obtient:
χ² = 2.5²*(2/22.5 + 2/77.5) = 0.717
Est-ce que cet écart est important ? On peut demander à R de calculer la probabilité d'excéder cette valeur avec la fonction 'pchisq':
obs<-c(25,20,75,80)
att<-c(22.5,22.5,77.5,77.5)
chi2<-sum((obs-att)**2/att)
chi2## [1] 0.71684591-pchisq(chi2,df=1)## [1] 0.3971805Dans la dernière ligne de code, la fonction 'pchisq(chi2,df=1)' calcule la probabilité Pr(x ≤ chi2) sachant que X a une distribution de χ² avec 1 degré de liberté (voir cours de statistique). Comme on est intéressé par la probabilité Pr(x > chi2) = 1 - Pr(x ≤ chi2), c'est ce calcul qui est réalisé, et qui fournit une probabilité de l'ordre de 40 %. En conclusion, il n'est pas rare de s'écarter aussi fort, voire plus fort, de ce qui était attendu, et on a donc pas de raison particulière de ne pas accepter l'hypothèse d'inocuité. Si on s'était fixé un seuil α = 5 % en deça duquel on aurait considéré qu'on doutait de l'hypothèse nulle, et donc qu'on la rejettait. La valeur de chi2 à atteindre pour arriver à cette conclusion de rejet peut également se calculer avec la fonction 'qchisq':
alpha<-0.5
qchisq(1-alpha,df=1)## [1] 0.4549364VI. Distributions continues: normales, t de Student, F de Snedecor
Les distributions continues s'utilisent de la même manière que les distributions discrètes vues plus haut. Nous les emploierons pour faire des calculs de probabilité (normales, t, F) et pour générer des données (essentiellement, distributions normales). Pour illustrer ces différentes fonctionnalités, nous allons générer des données de la manière suivante:
- La variable X représente l'âge en mois, et prend des valeurs entre 0 et 10
- La variable Y représente le poids, qui varie en moyenne linéairement avec l'âge: E[Y|X] = α + β*X où α et β sont deux paramètres à identifier
- Chaque individu s'écarte (en + ou en moins) de la moyenne d'une grandeur e, que nous supposerons tirée d'une distribution normale de moyenne 0 et de variance σ²
Commençons donc par générer 20 couples de valeurs (X,Y) en prenant pour paramètres α = 200, β = 100 et σ² = 100². Le code est le suivant:
X<-0:10
Y<-200+100*X+rnorm(11,mean=0,sd=100)La fonction "rnorm" est donc utilisée pour tirer au hasard des déviations autour de la droite moyenne représentant la relation entre les deux variables X et Y. On peut évidemment facilement représenter graphiquement les résultats obtenus en utilisant l'instruction "plot(X,Y)", ce qui conduit à:
plot(X,Y)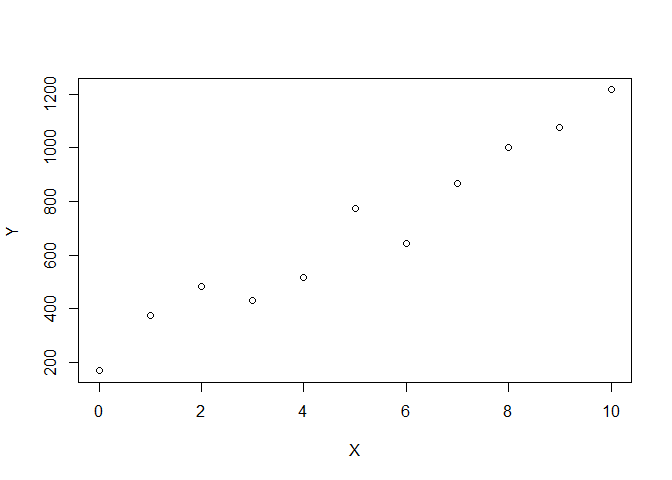
Dans le cours de statistique, on montre que cet ensemble de points peut être approximé par une droite d'équation:
Y = Yb + b * (X - Xb) = (Yb - b*Xb) + b*X
où Xb représente la moyenne des valeurs de X, Yb la moyenne des valeurs de Y, et b est un coefficient, appelé coefficient de régression de Y sur X, qui se calcule comme b = [Σ (X - Xb) * (Y - Yb)] / [Σ (X - Xb) * (X - Xb)]. Effectuons donc ces calculs, et montrons la droite correspondante dans le graphique:
Xb<-mean(X)
Yb<-mean(Y)
b<-sum((X-Xb)*(Y-Yb))/sum((X-Xb)*(X-Xb))
b## [1] 96.23533a<-Yb-b*Xb
a## [1] 205.2792oldpar<-par()
plot(X,Y)
par(fg="red")
abline(a,b)
par(fg="green")
abline(200,100)
par(oldpar)
Remarquez que, dans le calcul de b, on a utilisé plusieurs "trucs" de R: on soustrait un scalaire à un vecteur, ce qui revient à soustraire le scalaire à chaque élément du vecteur, on fait le produit de deux vecteurs, ce qui donne un vecteur dont les éléments sont le produit des éléments correspondants des deux vecteurs initiaux, et on utilise la fonction 'sum' sur un vecteur, ce qui donne un nombre scalaire égal à la somme des éléments du vecteur. Remarquez également que les résultats obtenus pour a et b sont assez proches des valeurs 100 et 200 utilisées pour α et β pour générer les données. La dernière instruction montre à quoi ressemblent la droite calculée (en rouge) et la droite utilisée pour générer les données (en vert).Le graphique devient:
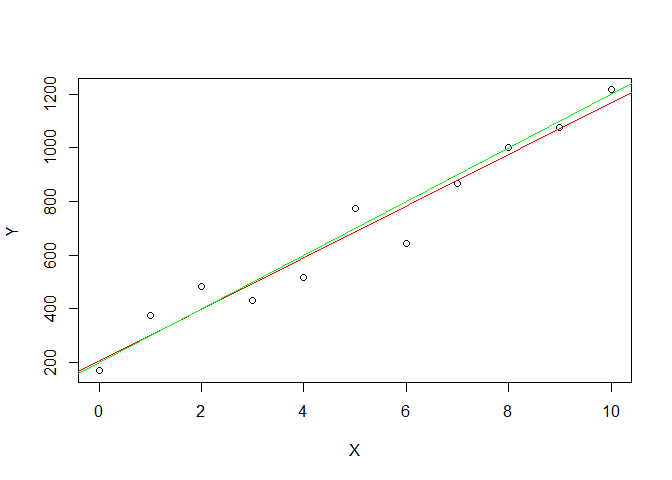
On voit que, dans cet exemple, les données ont permis d'estimer l'équation d'une droite assez proche de celle qui a réellement servi à générer les données. Ce n'est pas toujours le cas, et se pose alors la question de savoir si la droite estimée a un sens. En effet, il est toujours possible de prendre une série de n valeurs de X, une série de n valeurs de Y sans lien avec les valeurs de X et de suivre la procédure décrite ci-dessus. On montre dans le cours de statistique qu'il est possible de tester la signification de ce qu'on a obtenu en calculant la valeur de t = b*(n-2)* [Σ x * y] / [Σ (y - b*x)²] et en calculant la probabilité d'obtenir une valeur supérieure ou égale à t en utilisant la distribution t de Student avec (n-2) degrés de liberté. Dans l'expression de t, n est le nombre de couples (X,Y), soit 11 dans l'exemple, x = X - Xb et y = Y - Yb. Effectuons donc le calcul de t et le calcul de la probabilité de dépasser cette valeur de t s'il n'existe en réalité aucune liaison linéaire entre X et Y:
n<-11
x<-X-mean(X)
y<-Y-mean(Y)
b<-sum(x*y)/sum(x**2)
t<-b*(n-2)*sum(x*y)/sum((y-b*x)**2)
t## [1] 169.871-pt(t,n-2)## [1] 0On constate que la probabilité d'avoir une valeur supérieure ou égale à celle observée est excessivement faible: la conclusion est qu'on a très vraisemblablement obtenu cette valeur élevée de t parce que l'hypothèse qu'il n'existe pas de relation linéaire entre X et Y n'est pas correcte. On en déduit qu'il existe donc bien une relation linéaire entre ces deux variables. On remarquera également que le nom de la fonction est donc simplement 't', et les préfixes habituels sont utilisables:
d|p|q|r t(valeur, degrés de liberté)
La signification du second paramètre, "degrés de liberté", sera donnée au cours de statistiques.
La distribution de F s'emploie dans divers contextes dans le cours de statistiques. Son utilisation dans R sera similaire à celle qui vient d'être faite avec t: on l'utilisera essentiellement avec le préfixe 'p' pour calculer la probabilité d'obtenir la valeur de F qu'on a obtenue en partant de l'hypothèse que l'effet testé n'est pas présent. S'il s'avère que la valeur obtenue est alors peu probable (par exemple, a une probabilité inférieure à 0.05), on choisira de ne pas croire en l'hypothèse d'absence d'effet, ce qui revient à dire qu'on pense qu'il y a bel et bien un effet. De nombreux exemples seront donnés dans le cours de statistique. Pour illustrer l'utilisation de la distribution de F, nous allons générer la table donnant les limites que cette distribution ne dépasse que dans 1 % des cas (voir dans le cours de statistiques pour trouver cette table). Nous ferons donc varier les deux paramètres de la distribution de 1 à 10, et pour chaque combinaison calculerons la probabilité correspondant au seuil de 1 %. Voici le code:
alpha<-0.01
F<-matrix(0,nrow=10,ncol=10)
for(df1 in 1:10){
for(df2 in 1:10){
F[df1,df2]<-qf(1-alpha, df1, df2)
}
}
F## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 4052.181 98.50251 34.11622 21.19769 16.25818 13.745023 12.246383 11.258624 10.561431 10.044289
## [2,] 4999.500 99.00000 30.81652 18.00000 13.27393 10.924767 9.546578 8.649111 8.021517 7.559432
## [3,] 5403.352 99.16620 29.45670 16.69437 12.05995 9.779538 8.451285 7.590992 6.991917 6.552313
## [4,] 5624.583 99.24937 28.70990 15.97702 11.39193 9.148301 7.846645 7.006077 6.422085 5.994339
## [5,] 5763.650 99.29930 28.23708 15.52186 10.96702 8.745895 7.460435 6.631825 6.056941 5.636326
## [6,] 5858.986 99.33259 27.91066 15.20686 10.67225 8.466125 7.191405 6.370681 5.801770 5.385811
## [7,] 5928.356 99.35637 27.67170 14.97576 10.45551 8.259995 6.992833 6.177624 5.612865 5.200121
## [8,] 5981.070 99.37421 27.48918 14.79889 10.28931 8.101651 6.840049 6.028870 5.467123 5.056693
## [9,] 6022.473 99.38809 27.34521 14.65913 10.15776 7.976121 6.718752 5.910619 5.351129 4.942421
## [10,] 6055.847 99.39920 27.22873 14.54590 10.05102 7.874119 6.620063 5.814294 5.256542 4.849147