Créer des graphiques
Une des fonctionnalités majeures de R est son aptitude à créer de nombreux graphiques. Le chapitre qui suit va présenter une des fonctions principales à ce titre, la fonction 'plot'. D'autres exemples seront également donnés pour illustrer quelques autres facilités proposées par le logiciel.
I. Les fonctions 'plot' et 'boxplot'
L'usage de base de la fonction 'plot' est de représenter une série de données de manière graphique. Un petit dessin valant mieux qu'un long discours, nous allons immédiatement illustrer l'utilisation basique de la fonction sur un exemple:
x<-rnorm(20,mean=100,sd=10)
plot(x)
L'exécution de ces deux commandes conduit à l'ouverture d'une fenêtre contenant un graphique représentant l'échantillon aléatoire de 20 individus pris dans une distribution normale de moyenne 20 et de déviation standard 10.
Dans ce graphique bi-dimensionnel, l'abscisse est simplement la position de la valeur en ordonnée dans l'échantillon (de 1 à 20). Lorsqu'on veur voir sur un graphique la relation entre deux variables continues X et Y, on peut également utiliser cette même fonction de la manière montrée ci-dessous. Pour illustrer cette possibilité, nous allons générer des données (X,Y) corrélées en commençant par générer des données (U,V) non corrélées, puis en construisant X et Y à partir de U et V de la manière indiquée. On peut montrer qu'alors, la corrélation entre X et Y vaut ρ.
Voici le code:
u<-rnorm(100)
v<-rnorm(100)
cor(u,v) # calcul du coefficient de corrélation de Pearson## [1] 0.1176952rho<-0.6 # On va imposer un coefficient de corrélation de ρ =0.6
x<-0.5*(1+rho)*u+0.5*(1-rho)*v
y<-0.5*(1+rho)*u-0.5*(1-rho)*v
cor(x,y) # calcul du coefficient de corrélation de Pearson## [1] 0.8999611Cette première instruction 'plot' ouvre une fenêtre affichant un graphique X-Y avec des données non corrélées (ρ = 0.0, r = -0.01643519):
plot (u,v)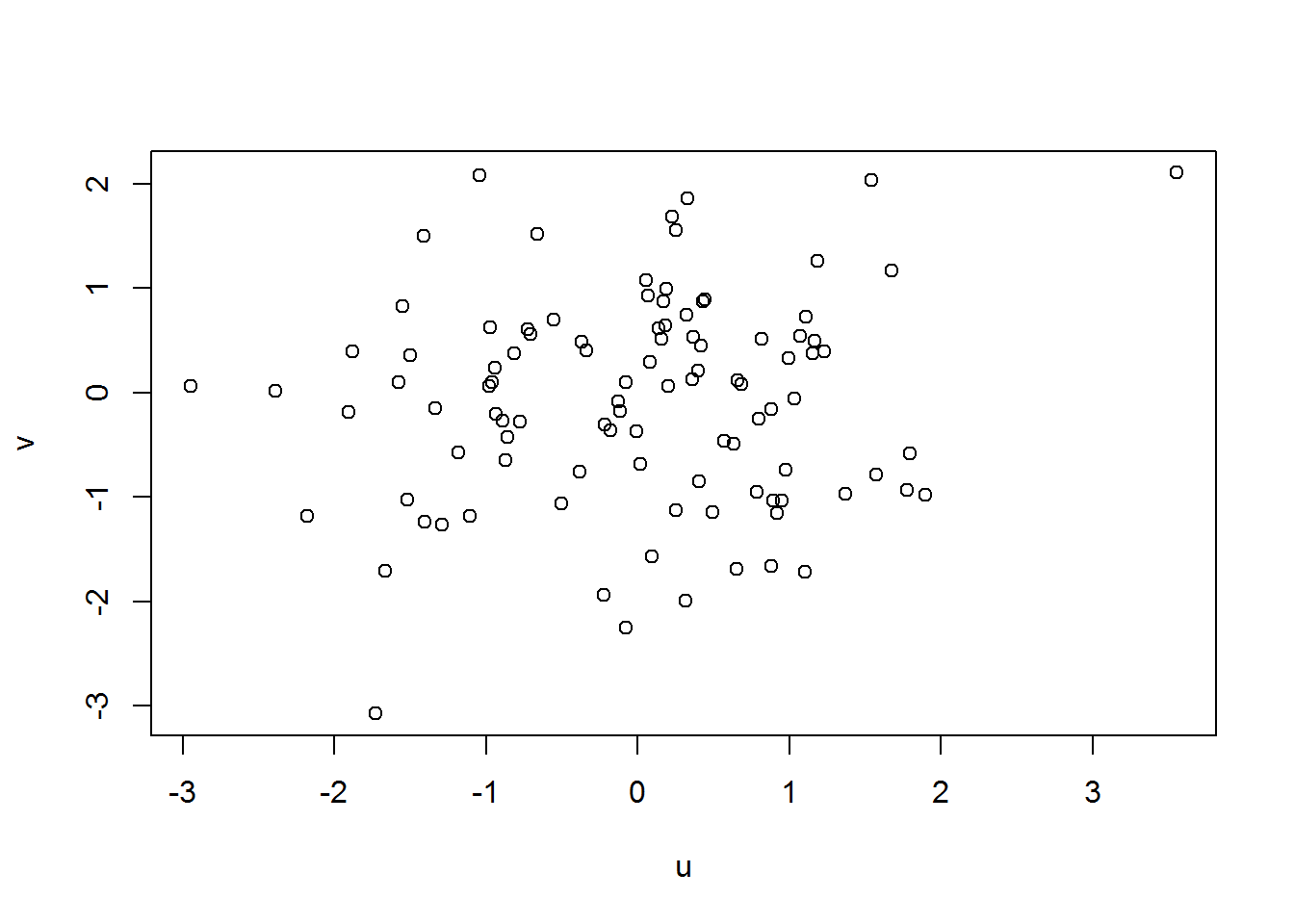
Et cette seconde instruction 'plot' donne un graphique X-Y avec des données corrélées (ρ = 0.6, r = 0.8629228):
plot (x,y)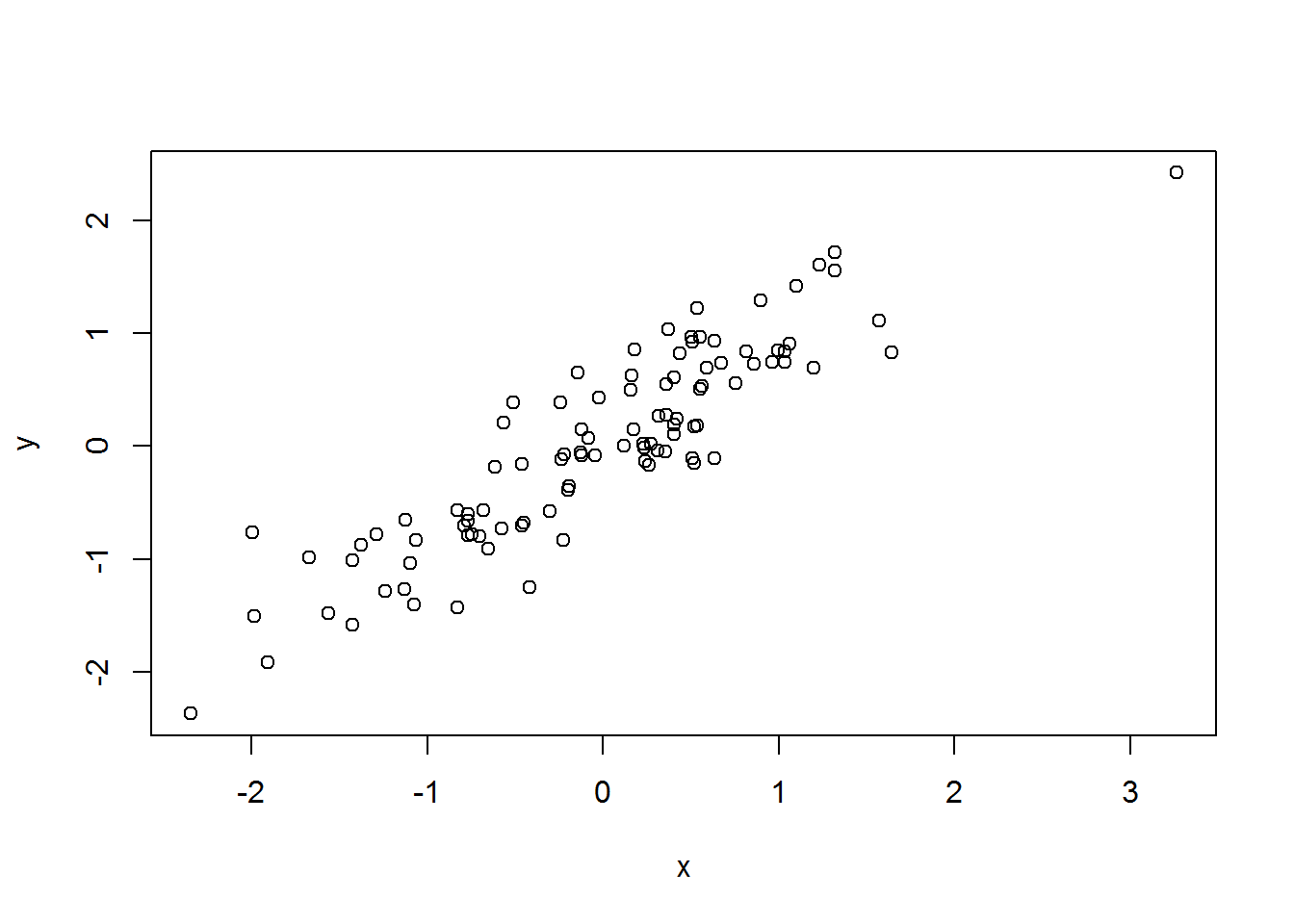
Une alternative à la fonction 'plot' est d'utiliser la fonction 'boxplot' pour obtenir un graphique de type box-plot (évidemment...). L'illustration est encore une fois très simple:
weight<-c(rnorm(10,mean=30,sd=5),rnorm(10,mean=25,sd=5)) # 'weight' est une variable continue
boxplot(weight)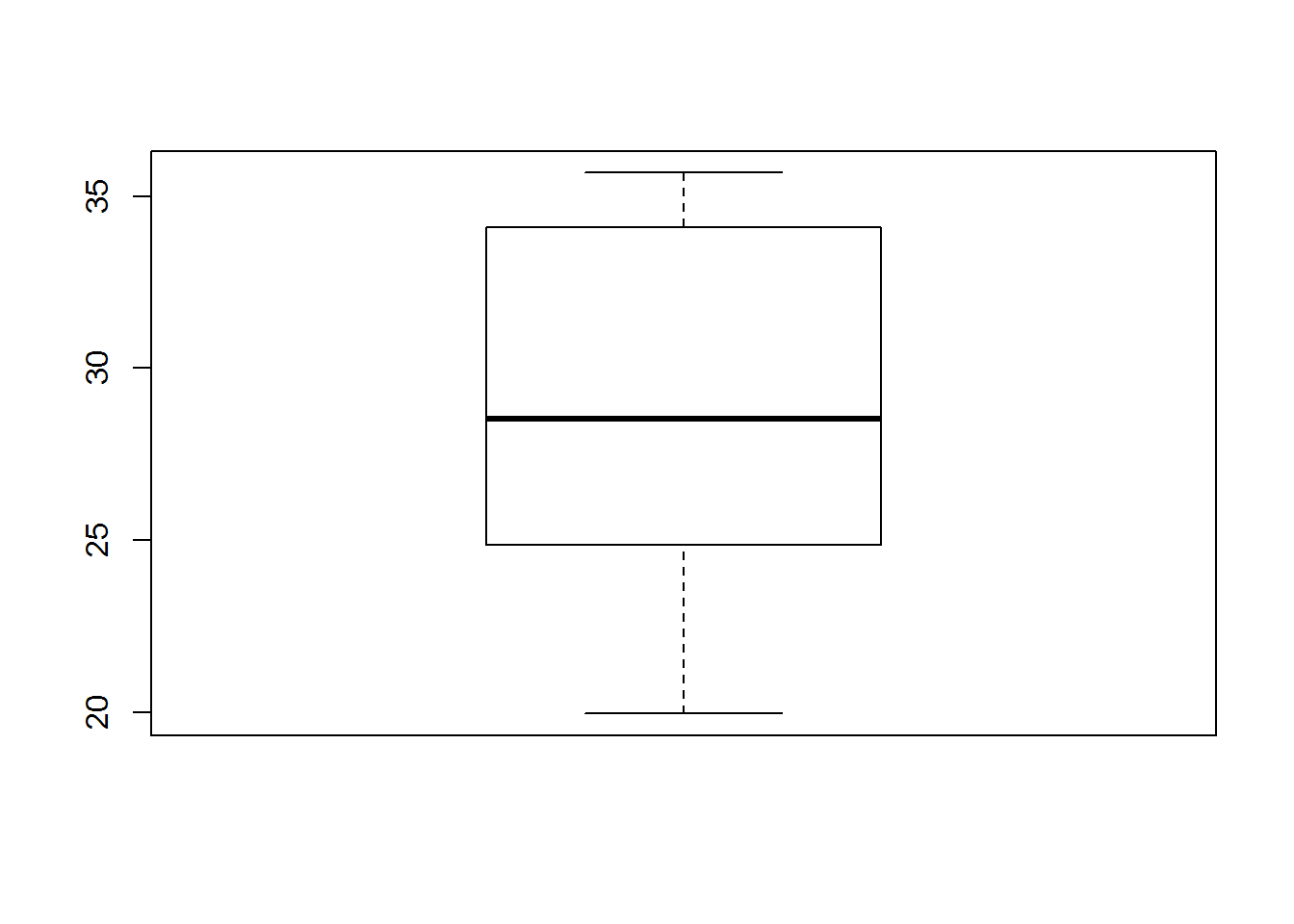
On peut voir que l'échantillon de poids est en réalité constitué de 2 échantillons de taille 10 provenant de deux distributions normales de moyennes respectives 30 et 25 et de déviation standard 5. On pourrait vouloir représenter un box-plot par catégorie (femelle ou mâle).
Une manière très simple de procéder est la suivante:sex<-c(rep("M",10),rep("F",10)) # 'sex' est une variable discrète
boxplot(weight~sex)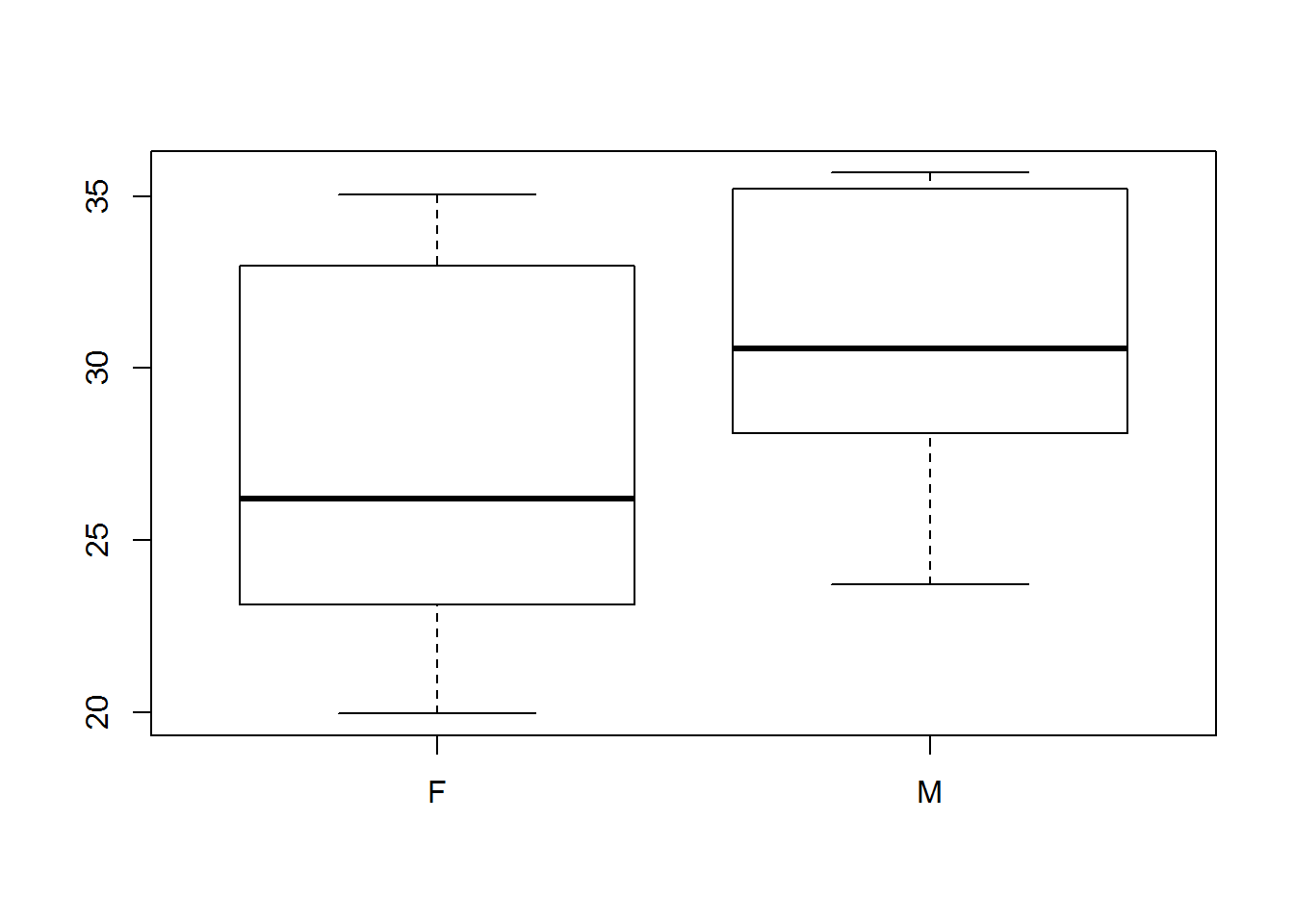
II. Paramètres graphiques
La manipulation de la plupart des paramètres graphiques (couleurs, titres, étiquetage des axes, etc...) peut se faire via la fonction 'par', qui a la forme:
par(<tag> = <value>, ...)
Dans cette définition, <tag> désigne un des paramètres graphiques et <value> la valeur qu'on souhaite lui donner. Une liste complète des paramètres avec leur valeur peut êtr obtenue en tapant:
par()## $xlog
## [1] FALSE
##
## $ylog
## [1] FALSE
##
## $adj
## [1] 0.5
##
## $ann
## [1] TRUE
##
## $ask
## [1] FALSE
##
## $bg
## [1] "white"La liste a été raccourcie dans la réponse pour limiter l'espace, car la liste est relativement longue. Nous allons dans ce qui suit donner un exemple d'utilisation de cette fonction 'par'. Notez encore que les changements de paramètres peuvent dans certains cas être spécifiés dans la fonction graphique elle-même.
x<-1:10
y<-3+2*x+rnorm(10)
par(col.axis="red",bg="grey")
plot(x,y,fg="blue")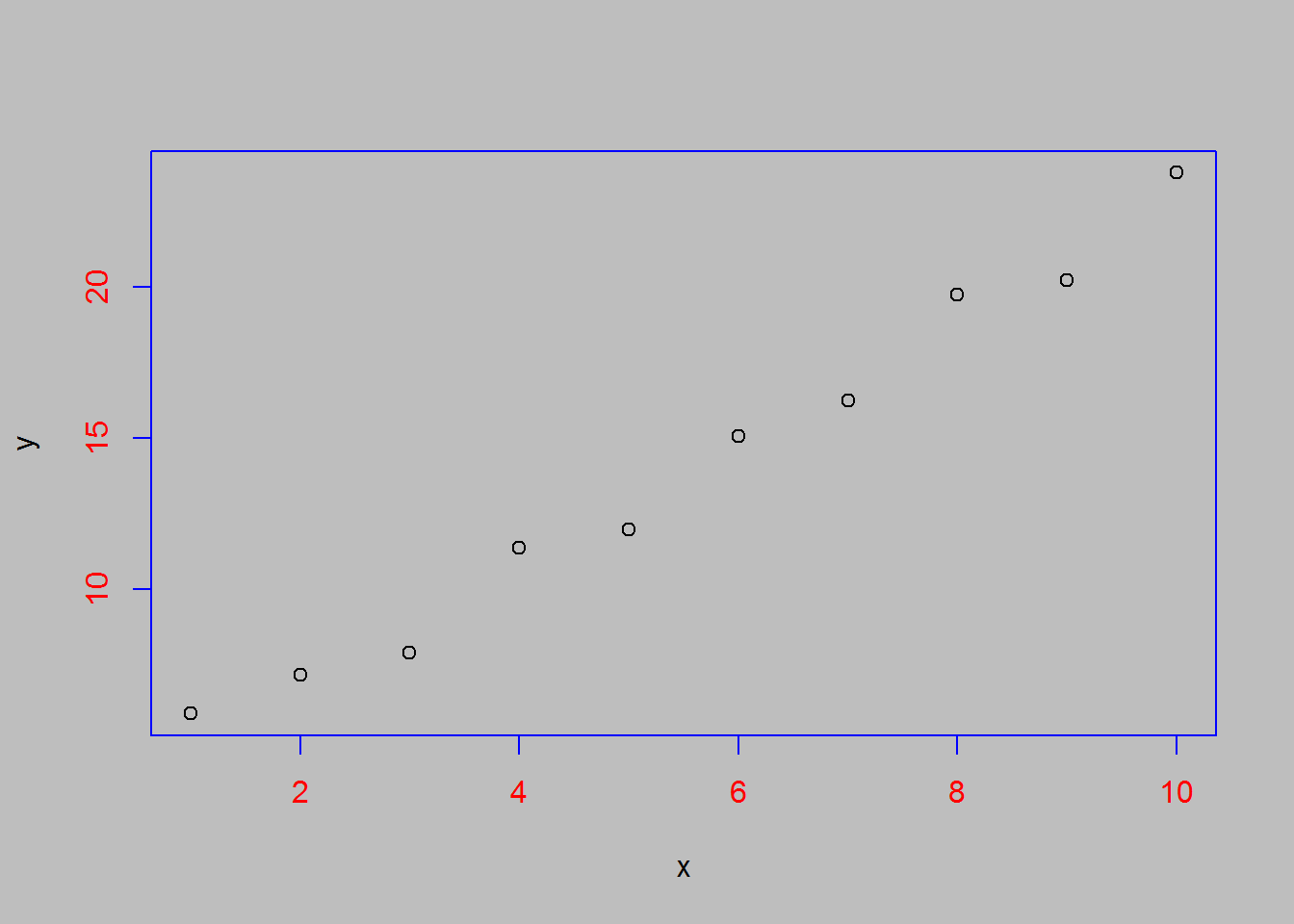
Il arrive également fréquemment qu'on souhaite temporairement modifier certains paramètres graphiques, puis restaurer pour la suite les anciens paramètres. Une manière de faire ça est la suivante: on mémorise les anciens paramètres dans une variable, on modifie les paramètres temporairement et on les utilise, puis on recopie les anciens paramètres. En termes de code R, on peut procéder comme suit:
anciens_par<-par() #Mémorisation des anciens paramètres dans une variable
par(fg="blue") #Modification des paramètres par un ou plusieurs appels à 'par'
plot(x,y) #Fonction graphique utilisant les nouveaux paramètres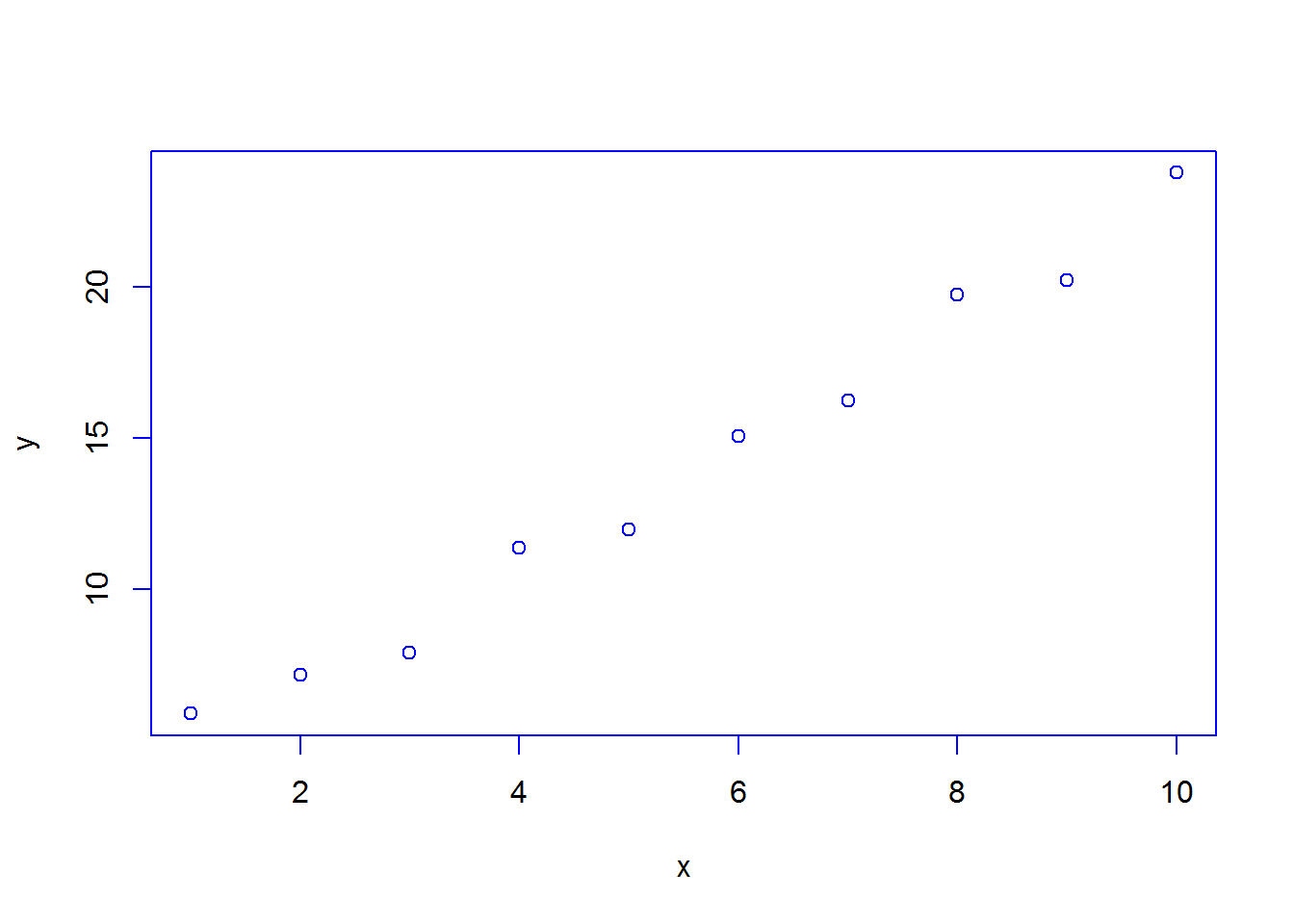
par(anciens_par) #Restauration des anciens paramètres graphiquesIII. D'autres fonctions graphiques
Il existe de nombreuses autres fonctions permettant de créer des graphiques. Il existe également des fonctions qui permettent de modifier le graphique en cours. Comme il est difficile d'être exhaustif dans cette courte introduction, nous allons donner deux exemples pour chaque catégorie de fonctions.
Commençons donc par deux fonctions qui modifient un graphique déjà créé:A. La fonction 'abline'
Cette fonction permet d'ajouter une ligne (par exemple, la droite de régression calculée) sur un graphique. La syntaxe est la suivante:
abline(a=<valeur>,b=<valeur>,h=<valeur>,v=<valeur>,...)
Les paramètres, qui ne contiennent rien par défaut, permettent de spécifier les paramètres de la droite: soit en spécifiant a et b pour afficher la droite d'équation Y = a + b*X, soit en spécifiant h pour une droite horizontale, soit en spécifiant v pour une droite verticale. Voici un exemple de code qui génère aléatoirement des points variant de manière normale autour d'une droite d'équation Y = 3 - 2*X. La droite est également représentée, ainsi que les deux droites X = X moyen et Y = Y moyen.
X<-1:10
Y<-3-2*X+rnorm(10,mean=0,sd=2)
oldpar<-par() #Sauvetage des paramètres graphiques
plot(X,Y)
abline(a=3,b=-2,col="green")
abline(v=5.5,col="red")
abline(h=mean(Y),col="red")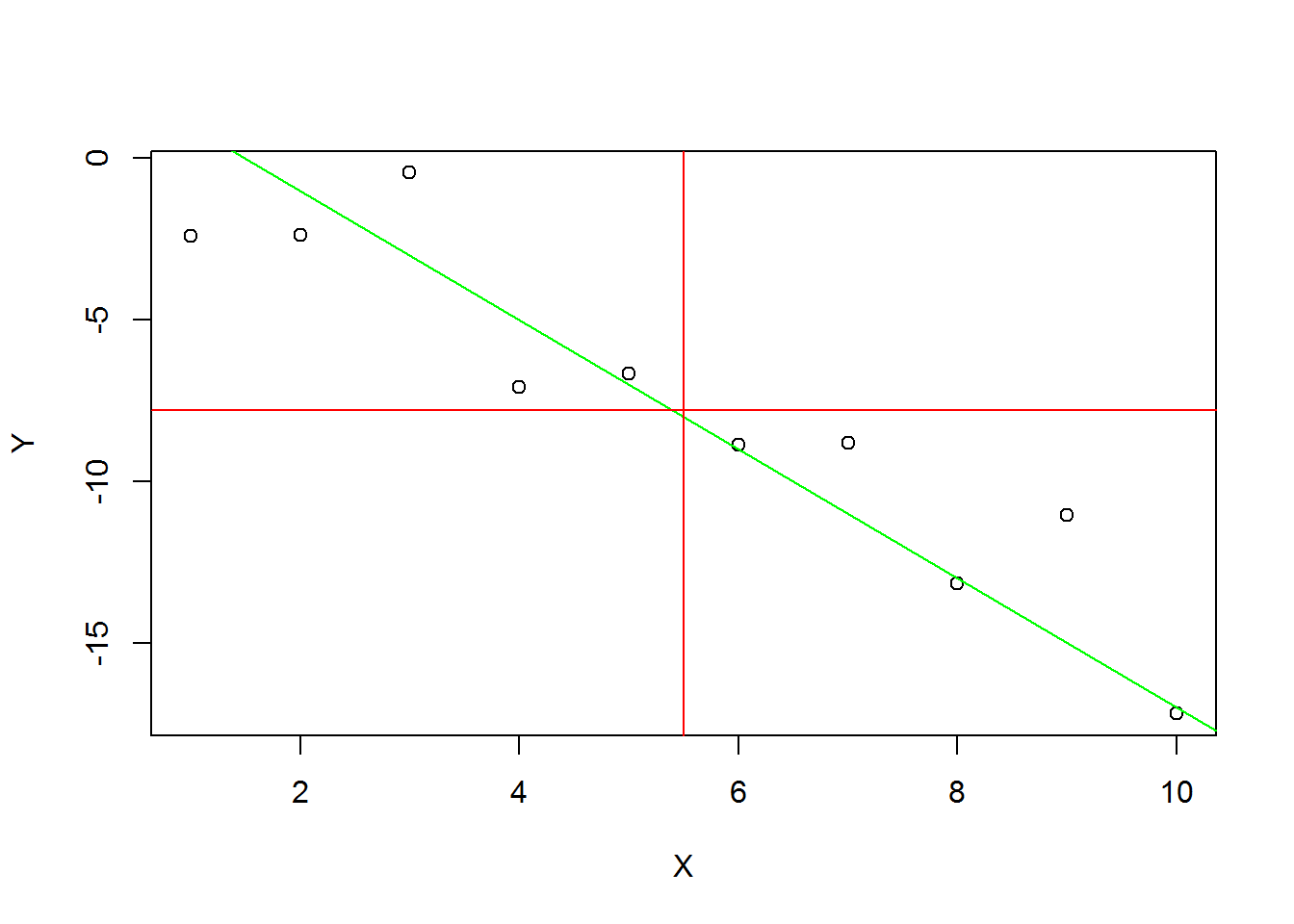
par(oldpar) #Restauration des paramètres graphiquesB. La fonction 'title'
On peut ajouter un titre au graphique avec la fonction 'title'. Les options principales s'utilisent selon la syntaxe:
title(main=<titre principal>,sub=<titre annexe>,...)
Continuant le code utilisé dans le paragraphe précédent, on pourrait écrire:
X<-1:10
Y<-3-2*X+rnorm(10,mean=0,sd=2)
oldpar<-par() #Sauvetage des paramètres graphiques
plot(X,Y)
abline(a=3,b=-2,col="green")
abline(v=5.5,col="red")
abline(h=mean(Y),col="red")
par(oldpar) #Restauration des paramètres graphiques
title(main="Régression de Y sur X", sub="Cours de R")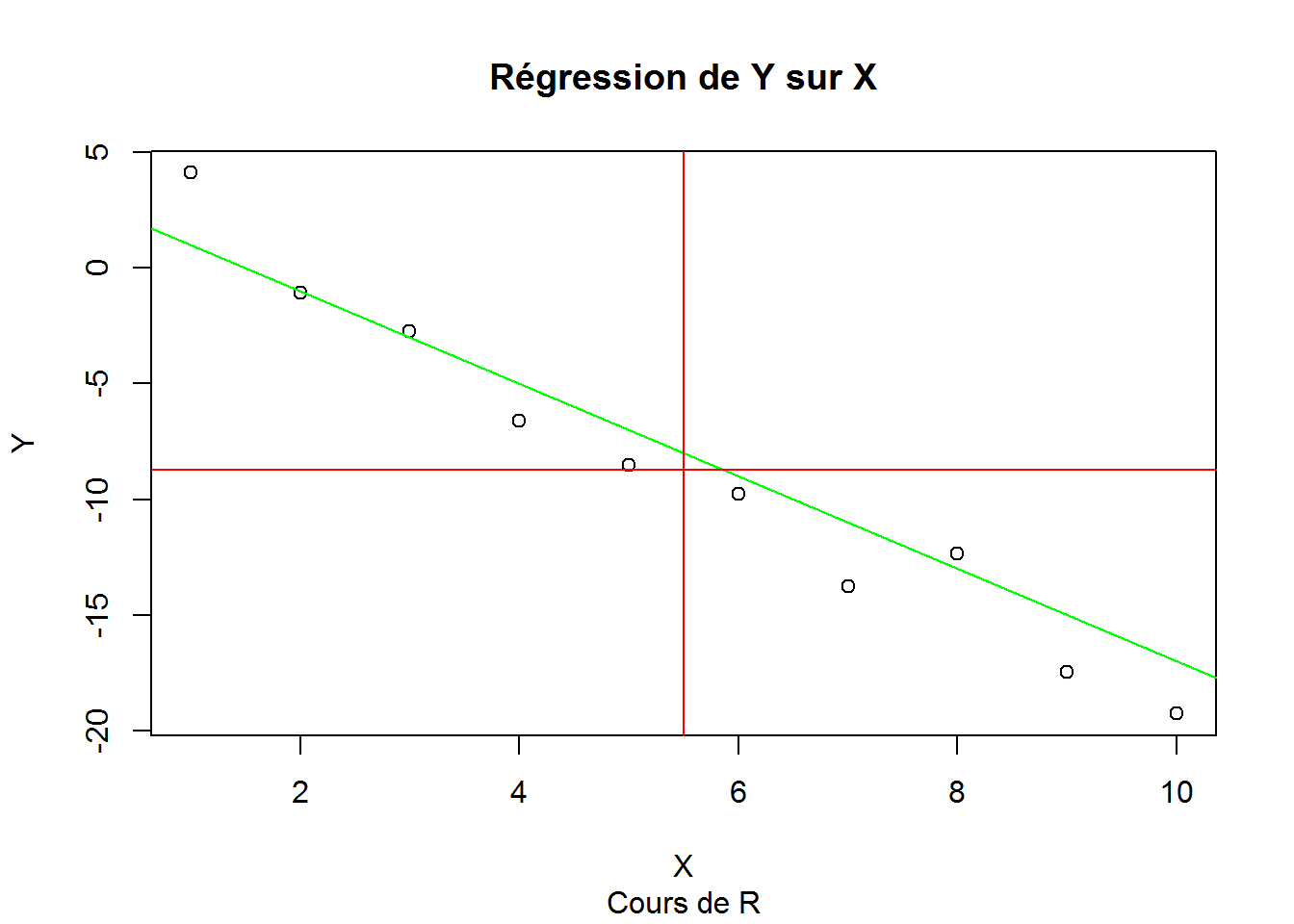
Montrons à présent deux autres exemples de fonctions graphiques:
C. La fonction 'stripchart'
Cette fonction permet de faire un graphique de dispersion lorsqu'on a une seule variable. Les valeurs sont alignées sur un axe, et les régions les plus probables sont matérialisées par le fait que la densité en points y augmente. On peut illustrer cette fonction en utilisant comme valeurs de la variable aléatoire un échantillon pris dans une distribution normale.
ech<-rnorm(200, mean=100,sd=20)
stripchart(ech)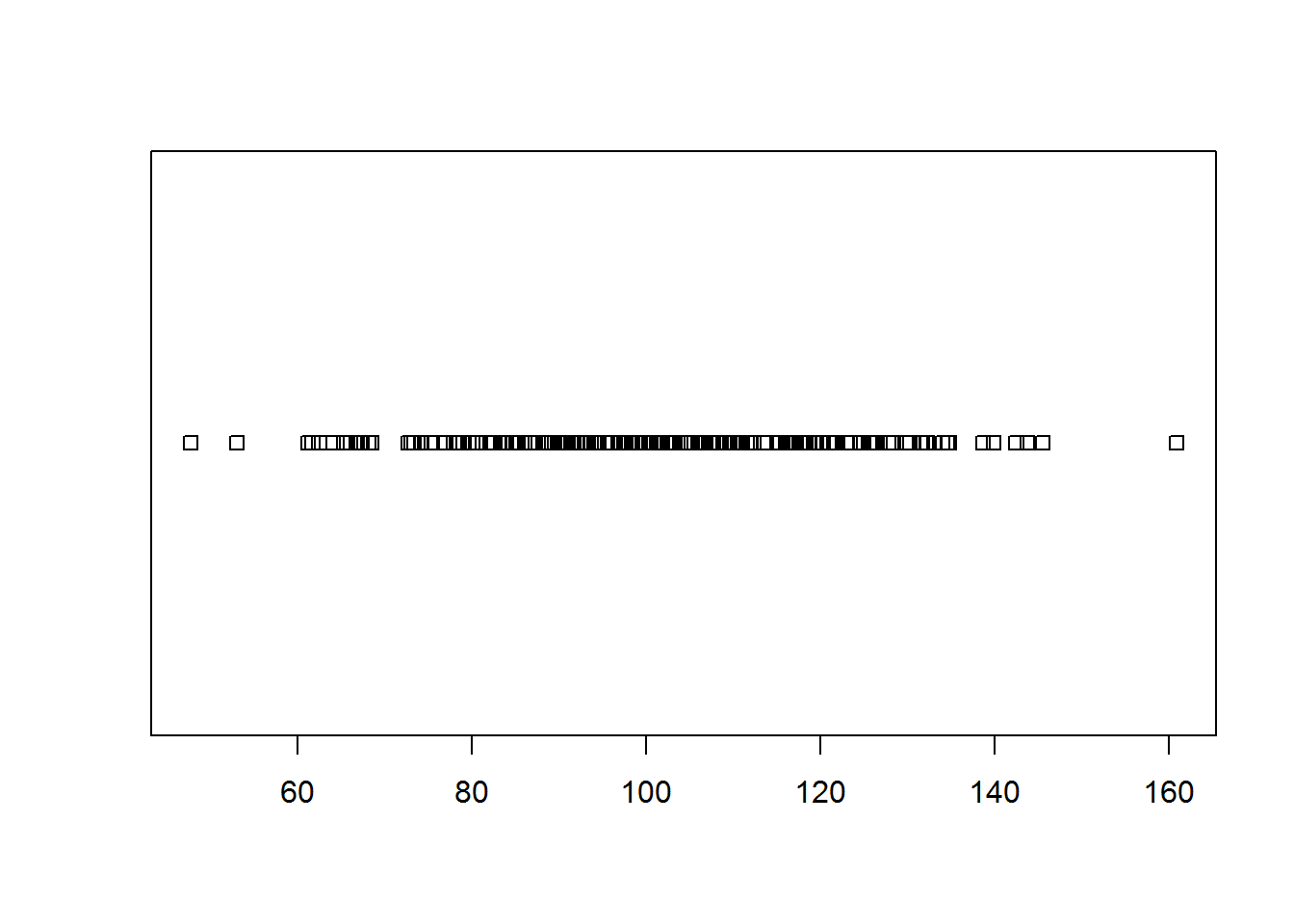
Le graphique est donc composé de petits carrés positionnés comme les valeurs correspondantes de X, et la superposition des carrés dans la région centrale visualise le fait qu'il y a plus de valeurs dans cette région, proche de la moyenne, que dans les extrémités droites et gauches. Si on souhaite mieux visualiser les observations, on peut demander à R d'empiler les observations identiques plutôt que de les superposer, avec l'option 'method="stack"'. Si on essaie le code avec cette option, le graphique ne se modifie pas. Pourquoi ? Tout simplement parce que R empilerait les valeurs identiques, mais il n'en trouve aucune dans l'échantillon: elles diffèrent toutes, éventuellement après plusieurs chiffres derrière la virgule ! On peut "tricher" un petit peu pour obtenir le graphique: plutôt que d'afficher les valeurs dans l'échantillon, on va demander d'afficher ces valeurs arrondies; ainsi, deux valeurs comme 1.14543 et 1.12198 sont toutes les deux arrondies à la même valeur, soit 1.0, et les petits carrés correspondants seront donc empilés !
Essayons donc ce code:
ech<-rnorm(200, mean=100,sd=20)
stripchart(round(ech,0), method="stack")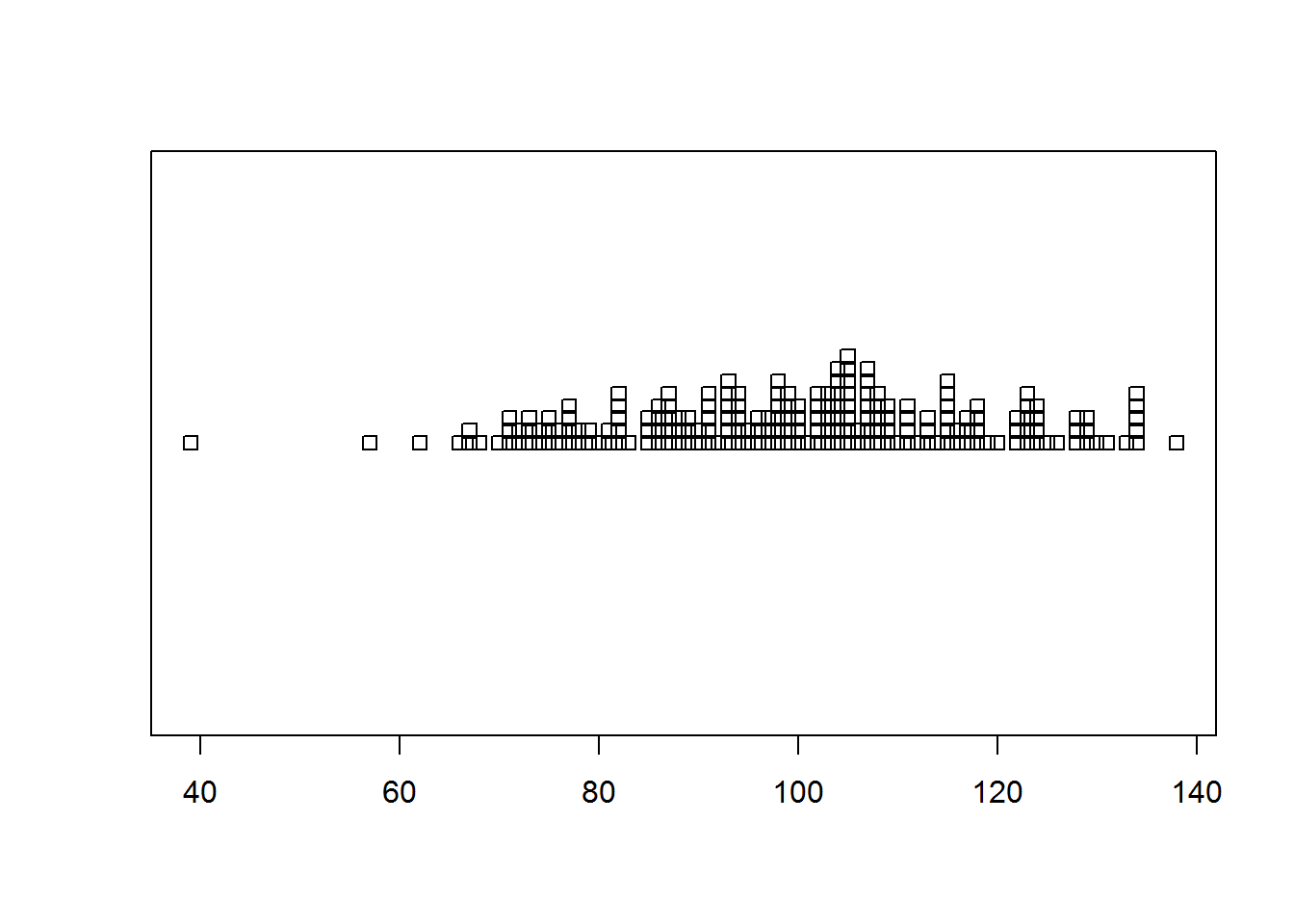
D. La fonction 'persp'
Lorsqu'on souhaite voir une perspective en 3D d'une fonction (typiquement à deux variables, z = f(x,y)), on peut utiliser la fonction 'persp(x,y,z)' où x, y et z sont trois vecteurs de même dimension. Les valeurs de z sont les valeurs correspondantes de f(x,y). Les valeurs de x et de y sont définies de la manière suivante: on donne l'ensemble des valeurs que peuvent prendre x et y (soit, respectivement, n et m valeurs). La fonction 'outer(x,y,f)' peut alors être utilisée pour générer tous les trios de valeurs de x, de y et de f(x,y).
Voici un exemple:plage_x<-1:4
plage_y<-seq(from=-2,to=2,length.out=6)
fxy<-function(x,y){x+y} #Cette fonction retourne la somme de ses arguments
outer(plage_x,plage_y,fxy)# [,1] [,2] [,3] [,4] [,5] [,6]
# [1,] -1 -0.2 0.6 1.4 2.2 3
# [2,] 0 0.8 1.6 2.4 3.2 4
# [3,] 1 1.8 2.6 3.4 4.2 5
# [4,] 2 2.8 3.6 4.4 5.2 6Utilisons une fonction plus compliquée pour effectuer le graphique et montrer quelques options de 'persp':
plage_x<-seq(-5,5,by=0.1)
plage_y<-plage_x
fxy<-function(x,y){exp(-(x**2+y**2)**0.5)*sin(x**2+y**2)}
persp(plage_x,plage_y,outer(plage_x,plage_y,fxy))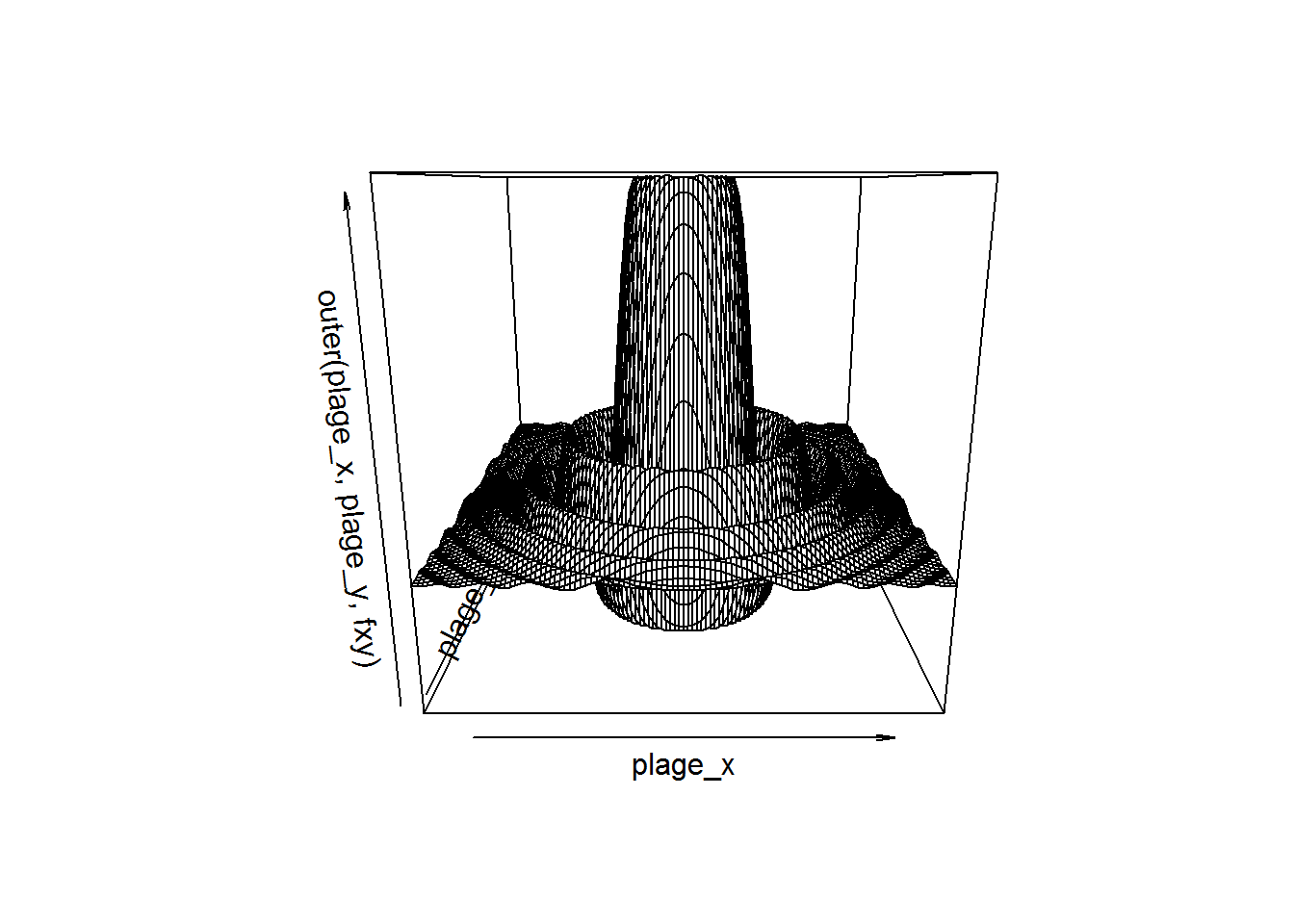
Pour mieux voir le graphe, on peut faire pivoter la courbe autour des axes en tapant:
persp(plage_x,plage_y,outer(plage_x,plage_y,fxy), theta=30, phi=30)
On peut encore améliorer le graphique en ajoutant d'autres options. Par exemple, on peut écrire ceci:
persp(plage_x,plage_y,outer(plage_x,plage_y,fxy), theta=30, phi=30,expand=0.5,col="lightgreen",shade=0.25,ticktype="detailed")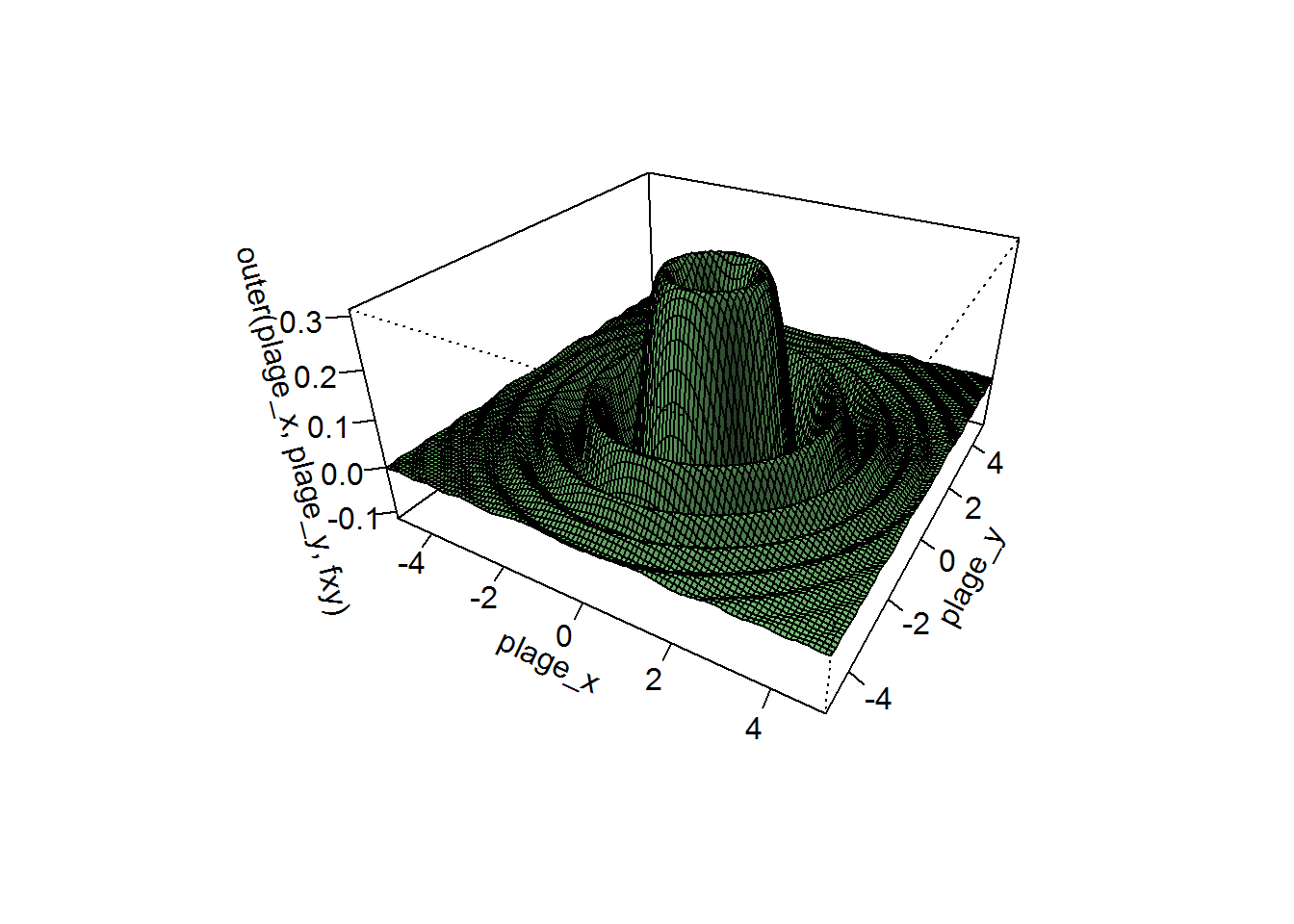
Il est possible de voir l'effet réel de chaque option individuellement en les ajoutant une à une et en regardant comment le graphique change à chaque étape.