Vérifier la normalité des données
Vérifier la normalité des données continues est une étape cruciale avant la réalisation d'un test d'hypothèse mettant en jeu une ou plusieurs variables continues. Il s'agit donc de s'assurer que les variables continues sont distribuées selon la loi normale. Si cela est le cas, les tests d'hypothèse classiques sont applicables. Si la condition de normalité est violée, il faudra trouver une alternative dite "non paramétrique" au test d'hypothèse à réaliser.
I. Approches empiriques et graphiques
Un examen préalable des données à l'aide de graphique ou de statistiques simples peuvent déjà permettre de visualiser si la distribution empirique suit une loi normale.
A. Histogramme de fréquence
On peut représenter les données à l'aide de l'histogramme de fréquence et regarder si elles semblent s'ajuster à une distribution normale.
Voici 2 exemples d'histogramme de fréquence avec en rouge le tracé de la densité de la loi normale.
poids1<-rnorm(30,10,2) # Création d'un échantillon de 30 poids provenant d'une distribution normale ayant pour moyenne 10 et pour écart-type 2
poids1## [1] 8.424638 7.992313 10.235702 10.922727 11.937969 9.317149 11.523925
## [8] 9.254642 9.566226 9.675670 8.271874 15.886934 13.519587 13.946394
## [15] 8.127138 8.682851 10.955421 10.499809 11.738918 10.714309 11.035992
## [22] 11.409635 7.647102 10.643227 9.232568 9.109664 12.852678 12.847700
## [29] 10.633125 9.107221hist(poids1, prob=T)
curve(dnorm(x,mean(poids1),sd(poids1)),add=T,col="red")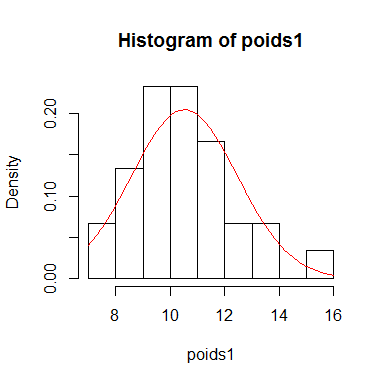
poids2<-c(runif(10,8,13),runif(20,13,15)) # Création d'un échantillon de 30 poids
poids2## [1] 9.756483 11.194571 9.459757 9.613224 11.884506 12.035321 11.582494
## [8] 10.851924 12.923106 9.937877 14.160016 14.348161 14.249056 14.038395
## [15] 14.565139 13.158117 14.783578 14.451904 13.325800 13.931306 14.868687
## [22] 13.599411 13.894222 13.988283 13.408088 14.672971 14.961377 13.218739
## [29] 14.116704 13.934829hist(poids2,prob=T)
curve(dnorm(x,mean(poids2),sd(poids2)), add=T,col="red")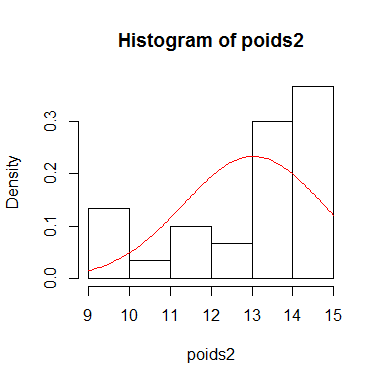
On observe que dans le premier cas, les données sont centrées et semblent s'ajuster à la courbe de la loi normale alors que dans le deuxième cas, les données sont plus dispersées et s'éloigne plus fortement de la loi normale.
B. Boîte à moustache
La boîte à moustache représente une distribution empirique à l'aide des quartiles: minimum, maximum, médiane, 1er quartile (Q1) et 3ème quartile (Q3). La boîte à moustache permet d'observer les valeurs extrêmes (outliers) mais également d'avoir une idée sur la symétrie de la distribution. La symétrie d'une distribution n'affirme pas la normalité, mais une distribution normale est forcément symétrique. Une boîte à moustache est dite symétrique lorsque la position de la médiane se situe au milieu de la boîte à moustache et qu'il y a symétrie des moustaches.
Reprenons nos deux exemples précédent:
boxplot(poids1, main="Poids 1")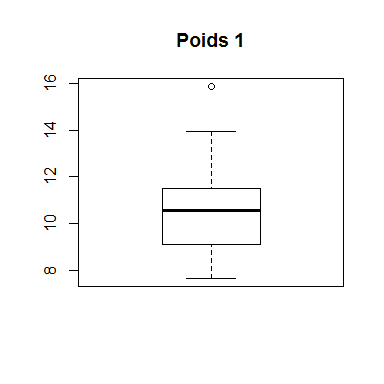
boxplot(poids2, main="Poids 2")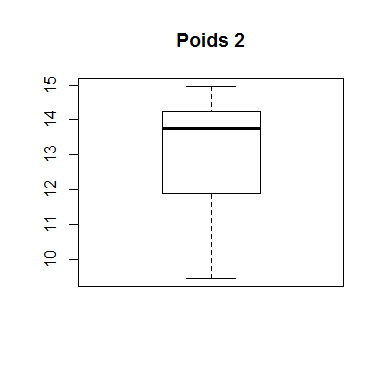
On observe, dans l'exemple 1, que la médiane se situe légèrement dans la partie supérieure de la boîte à moustache et que le minimum et le maximum sont légèrement asymétriques. Il y a également une mesure qui est fortement séparée des autres et qui pourrait être un outlier. Dans l'exemple 2, la médiane se situe à l'extrémité haute de la boîte à moustache et les moustaches sont fortement asymétriques.
C. Coefficient d'asymétrie et d'aplatissement
La loi normale est caractérisée par un coefficient d'asymétrie et un coefficient d'aplatissement nuls. Ces indicateurs peuvent donc également nous donner une idée, ne serait-ce que très approximative, du rapprochement possible de la distribution empirique avec une gaussienne.
- Le coefficient d'asymétrie
Le coefficient d'asymétrie se calcule à l'aide de la formule suivante:
\(\frac{n}{(n-1)(n-2)}*\sum (\frac{x-\bar{x}}{s})^3\)
Dans R, cela donne:
n<-length(poids1)
(n/((n-1)*(n-2)))*sum(((poids1-mean(poids1))/sd(poids1))^3)## [1] 0.7965753n<-length(poids2)
(n/((n-1)*(n-2)))*sum(((poids2-mean(poids2))/sd(poids2))^3)## [1] -0.9655081Les deux coefficients d'asymétrie sont assez éloignés de 0. Un coefficient d'asymétrie positif indique une asymétrie gauche, tandis qu'un coefficient d'asymétrie négatif indique une asymétrie droite.
- Le coefficient d'aplatissement
Le coefficient d'aplatissement se calcule à l'aide de la formule suivante:
\(\frac{n(n+1)}{(n-1)(n-2)(n-3)}*\sum(\frac{x-\bar{x}}{s})^4-\frac{3(n-1)^2}{(n-2)(n-3)}\)
Dans R, cela donne:
n<-length(poids1)
nc<-(n*(n+1))/((n-1)*(n-2)*(n-3))
sum<-sum(((poids1-mean(poids1))/sd(poids1))^4)
nc2<-3*((n-1)^2)/((n-2)*(n-3))
nc*sum-nc2## [1] 0.5797181n<-length(poids2)
nc<-(n*(n+1))/((n-1)*(n-2)*(n-3))
sum<-sum(((poids2-mean(poids2))/sd(poids2))^4)
nc2<-3*((n-1)^2)/((n-2)*(n-3))
nc*sum-nc2## [1] -0.3308675De nouveau, les deux coefficients sont éloignés de 0. Un coefficient d'aplatissement négatif indique que la distribution est "platykurtique", c'est-à-dire plus aplatie qu'une densité normale. Un coefficient d'aplatissement positif indique que la distribution est "leptokurtique", c'est-à-dire moins aplatie.
A partir de ces deux coefficients, on conclurait que ces deux jeux de données ne proviennent pas d'une distribution normale. Cela prouve qu'il est important de se baser sur plusieurs paramètres avant de décider de la normalité des données.
D. QQ-plot
Le "diagramme Quantile-Quantile" ou "diagramme Q-Q" ou "Q-Q plot" est un outil graphique permettant d'évaluer la pertinence de l'ajustement d'une distribution donnée à un modèle théorique. à partir de la série statistique observée, on calcule alors un certain nombre de quantiles. Si la série statistique suit bien la distribution théorique choisie, on devrait avoir les quantiles observés égaux aux quantiles associés au modèle théorique.
qqnorm(poids1, datax=TRUE, main="Poids1")
qqline(poids1,datax=TRUE)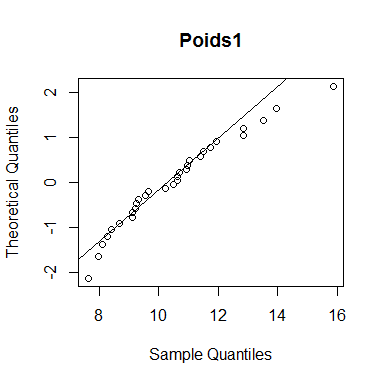
qqnorm(poids2,datax=TRUE, main="Poids2")
qqline(poids2,datax=TRUE)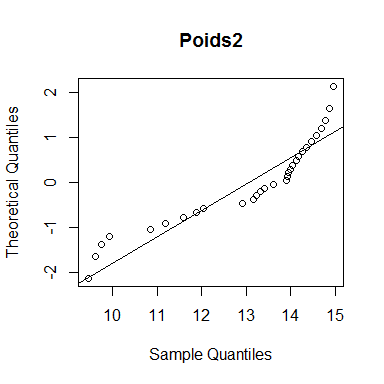
Plus les données (points) se rapprochent de la droite, plus la distribution empirique est dite normale. Les données de l'exemple 1 sont proches de la droite tandis que les données de l'exemple 2 sont plus éloignées.
II. Les tests statistiques:
Il existe plusieurs tests pour affirmer la normalité d'une distribution. Tous ces tests ont en commun d'avoir comme hypthèse nulle: La distribution empirique suit une loi Gaussienne.
A. Le test de Shapiro-Wilk
Un des tests permettant de vérifier la normalité de la variable x est le test de Shapiro-Wilk. Il est appliquable pour des échantillons allant jusqu'à 50 valeurs. Il utilise le rapport de deux estimations de la variance. Dans le cas d'une variable normale, ces deux estimations coïncident et le rapport est voisin de 1, alors que si la variable n'est pas normale le rapport est plus petit que 1.
Voici les différentes étapes pour calculer la valeur W du test de Shapiro-Wilk à partir d'un échantillon avec n observations: \(x_{1}, x_{2}, \dots, x_{n}\)
- On trie les observations dans l'ordre croissant: \(y_{1} \leq y_{2} \leq \dots \leq y_{n}\)
- On calcule la moyenne de ces observations: \(\bar{y} = \frac{1}{n} \displaystyle\sum_{i=1}^{n} y_{i}\)
- On calcule S² qui est la somme des écarts à la moyenne: \(S^2=\displaystyle\sum_{i=1}^{n} (y_{i}-\bar{y})^2\)
- On calcule b² (un autre estimateur de la variance des données):
- On cacule d: \(d_{i}=y_{n-i+1}-y_{i}\)
- Si n est pair, k=n/2. Si n est impair, k=(n-1)/2, ce qui signifie qu'on ignore la médiane dans le calcul b².
- \(b^2=\big(\displaystyle\sum_{j=1}^{k} (\alpha_{j}*d_{j})\big)^2\) où \(\alpha_{j}\) correspond aux valeurs de la table suivante: Table 1: Valeurs \(\alpha_{j}\) à utiliser pour calculer b².
- On calcule W: \(W=\frac{b^2}{S^2}\)
- On compare la valeur de W observée avec la valeur de W donnée dans la table suivante: Table 2: Valeurs critiques de W.
Si Wobs < W0.05, on rejette l'H0, ce qui indique la non normalité des données. - Trier les données
- Calculer les probabilités observées cumulées des valeurs de x
- Centrer et réduire les valeurs de x
- Calculer les probabilités théoriques des valeurs de x
- Calculer la différence entre les probabilités théoriques et empiriques
- Trouver la valeur maximale des différences et la comparer à la valeur critique D (trouvée dans la table suivante: Table 3: Valeurs critiques de D)
-Si Dmax < D0.05, l'H0 est tolérée: la distribution empirique semble correspondre à une distribution normale.
-Si Dmax > D0.05, l'H0 est rejetée: la distribution empirique ne provient pas d'une distribution normale.
Voici une application dans R à partir de nos deux exemples de poids:
Exemple 1
#Poids1
y<-sort(poids1)
m<-mean(poids1) #ce qui équivaut également à mean(y)
S<-sum((y-m)^2)
d<-0
n<-length(poids1)
for (i in 1:n){
d[i]=y[n-i+1]-y[i]
}
alpha<-c(0.4254,0.2944,0.2487,0.2148,0.1870,0.1630,0.1415,0.1219,0.1036,0.0882,0.0697,0.0537,0.0381,0.0227,0.0076) #correspond aux valeurs de la table 1 avec n=30
k<-n/2
b<-(sum(d[1:k]*alpha))^2
W<-b/S
W## [1] 0.9511669A présent, nous devons comparer cette valeur de W obtenue avec la valeur de W de la table 2. W0.05 avec n=30 équivaut à 0.927. Etant donné que Wobs > W0.05, on tolère l'H0. Les données suivent une distribution normale.
Exemple 2
#Poids2
y<-sort(poids2)
m<-mean(poids2) #ce qui équivaut également à mean(y)
S<-sum((y-m)^2)
d<-0
n<-length(poids2)
for (i in 1:n){
d[i]=y[n-i+1]-y[i]
}
alpha<-c(0.4254,0.2944,0.2487,0.2148,0.1870,0.1630,0.1415,0.1219,0.1036,0.0882,0.0697,0.0537,0.0381,0.0227,0.0076) #correspond aux valeurs de la table 1 avec n=30
k<-n/2
b<-(sum(d[1:k]*alpha))^2
W<-b/S
W## [1] 0.854205A présent, nous devons comparer cette valeur de W obtenue avec la valeur de W de la table 2. W0.05 avec n=30 équivaut à 0.927. Etant donné que Wobs < W0.05, on rejette l'H0. Les données ne suivent pas une distribution normale.
Il existe une commande dans R qui permet de calculer directement la valeur de Wobs et la probabilité de dépassement associée à cette valeur: shapiro.test(x)
Comme on peut le constater, cela correspond effectivement aux valeurs obtenues manuellement ci-dessus (à quelques décimales près) et aux conclusions tirées.
shapiro.test(poids1)##
## Shapiro-Wilk normality test
##
## data: poids1
## W = 0.95129, p-value = 0.1831Le test de Shapiro-Wilk donne une probabilité de dépassement de 0.1831, supérieure à 0.05. L'hypothèse de normalité est donc tolérée.
shapiro.test(poids2)##
## Shapiro-Wilk normality test
##
## data: poids2
## W = 0.85798, p-value = 0.000915Le test de Shapiro-Wilk donne une probabilité de dépassement de 0.0009, inférieure à 0.05. L'hypothèse de normalité est donc rejetée.
B. Le test de Kolmogorov-Smirnov
Le test de Kolmogorov-Smirnov permet de tester l'ajustement des données x à n'importe quelle loi, dont la loi normale. Il est intéressant d'opter pour ce test plutôt que celui de Shapiro-Wilk en cas de très grands échantillons. Ce test détermine si les observations d'un échantillon peuvent raisonnablement provenir d'une distribution théorique donnée.
Le principe est simple. On mesure l'écart maximum qui existe entre la fonction de répartition observée (ou tout simplement des fréquences cumulées) et la fonction de répartition théorique. Sous l'hypothèse H0, cet écart est faible et la répartition des observations s'intègre bien dans une distribution donnée. Le graphique ci-dessous permet de bien visualiser ce qu'on cherche à faire: La flèche verte mesure l'écart maximum entre les observations (en bleu) et la fonction de répartition connue en rouge. C'est cette distance D qui est testée: compte tenu de l'effectif, la longueur de cette flèche est-elle considéré comme "petite" ou "grande" ?
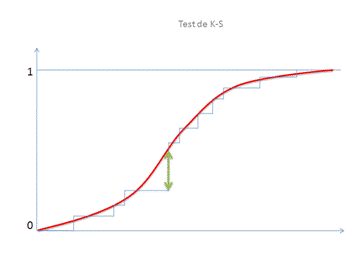
Voici comment le calculer manuellement:
Avec les données sur le poids, cela donne dans R:
Exemple 1:
#Poids1
#1. Trier les données par ordre croissant
x<-sort(poids1)
#2. Calculer les probabilités empiriques cumulées des valeurs de x
Cumul<-c(1:length(poids1))
S<-Cumul/length(poids1)
#3. Centrer et réduire les valeurs de x
z<-(x-mean(poids1))/sd(poids1)
#4. Calculer les probabilités théoriques des valeurs de x
F<-pnorm(z,0,1)
#5. Calculer la différence entre les probabilités théoriques et empiriques
Diff1<-abs(S-F)
Diff2<-c(F[1], rep(0,length(poids1)-1))
for (i in 2:length(poids1)){
Diff2[i]<-abs(S[i-1]-F[i])
}
d<-data.frame(x,Cumul,S,z,F, Diff1,Diff2)
d## x Cumul S z F Diff1 Diff2
## 1 7.647102 1 0.03333333 -1.47729010 0.06979895 0.0364656125 0.0697989458
## 2 7.992313 2 0.06666667 -1.30000970 0.09679882 0.0301321559 0.0634654893
## 3 8.127138 3 0.10000000 -1.23077168 0.10920414 0.0092041352 0.0425374685
## 4 8.271874 4 0.13333333 -1.15644341 0.12374992 0.0095834169 0.0237499165
## 5 8.424638 5 0.16666667 -1.07799282 0.14051848 0.0261481872 0.0071851461
## 6 8.682851 6 0.20000000 -0.94538958 0.17223001 0.0277699907 0.0055633427
## 7 9.107221 7 0.23333333 -0.72745778 0.23347279 0.0001394529 0.0334727863
## 8 9.109664 8 0.26666667 -0.72620316 0.23385712 0.0328095506 0.0005237827
## 9 9.232568 9 0.30000000 -0.66308661 0.25363754 0.0463624578 0.0130291245
## 10 9.254642 10 0.33333333 -0.65175086 0.25728095 0.0760523784 0.0427190450
## 11 9.317149 11 0.36666667 -0.61965096 0.26774380 0.0989228640 0.0655895307
## 12 9.566226 12 0.40000000 -0.49173911 0.31145189 0.0885481074 0.0552147741
## 13 9.675670 13 0.43333333 -0.43553508 0.33158704 0.1017462927 0.0684129594
## 14 10.235702 14 0.46666667 -0.14793522 0.44119695 0.0254697214 0.0078636119
## 15 10.499809 15 0.50000000 -0.01230518 0.49509107 0.0049089310 0.0284244024
## 16 10.633125 16 0.53333333 0.05615801 0.52239203 0.0109412996 0.0223920338
## 17 10.643227 17 0.56666667 0.06134617 0.52445824 0.0422084256 0.0088750923
## 18 10.714309 18 0.60000000 0.09784963 0.53897415 0.0610258494 0.0276925160
## 19 10.922727 19 0.63333333 0.20488128 0.58116756 0.0521657727 0.0188324394
## 20 10.955421 20 0.66666667 0.22167064 0.58771485 0.0789518117 0.0456184783
## 21 11.035992 21 0.70000000 0.26304747 0.60374300 0.0962569954 0.0629236621
## 22 11.409635 22 0.73333333 0.45492888 0.67541980 0.0579135367 0.0245802034
## 23 11.523925 23 0.76666667 0.51362168 0.69624174 0.0704249263 0.0370915929
## 24 11.738918 24 0.80000000 0.62402941 0.73369586 0.0663041357 0.0329708023
## 25 11.937969 25 0.83333333 0.72625049 0.76615739 0.0671759457 0.0338426124
## 26 12.847700 26 0.86666667 1.19343568 0.88365061 0.0169839387 0.0503172721
## 27 12.852678 27 0.90000000 1.19599233 0.88415022 0.0158497758 0.0174835575
## 28 13.519587 28 0.93333333 1.53847810 0.93803412 0.0047007871 0.0380341204
## 29 13.946394 29 0.96666667 1.75766139 0.96059743 0.0060692369 0.0272640964
## 30 15.886934 30 1.00000000 2.75421010 0.99705830 0.0029416994 0.0303916340
D1<-sort(Diff1)
D2<-sort(Diff2)
Dmax<-c(D1[length(D1)],D2[length(D2)])
Dmax## [1] 0.10174629 0.06979895Selon la table 3 ci-dessus, la valeur de D0.05 = 0.240 (pour n = 30). Etant donné que Dmaxobs (0.10174629) < D0.05 (0.240), l'H0 est tolérée.
Voici la représentation graphique du calcul de Dmax:
#Graphique
x2<-0
if (Dmax[1]>Dmax[2]){
for (i in 1:length(poids1)){
if (Diff1[i]==Dmax[1]) {
x2<-x[i]
}
}}
if (Dmax[1]<Dmax[2]){
for (i in 1:length(poids1)){
if (Diff2[i]==Dmax[2]) {
x2<-x[i]
}
}}
x2 #valeur de x de la plus grande différence entre les distributions théorique et empirique## [1] 9.67567plot(d$x,d$S, type="l", main="Poids1")
lines(d$x,d$F,col="red")
abline(v=x2, col="blue")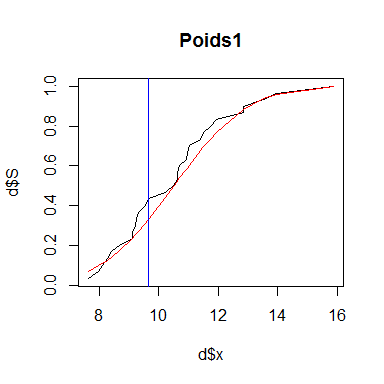
La courbe noire est la distribution cumulée observée tandis que la courbe rouge est la distribution cumulée théorique. La ligne bleue indique Dmax, c'est-à-dire l'endroit où l'écart entre les données observées et théoriques est le plus important.
Exemple 2:
#Poids2
#1. Trier les données par ordre croissant
x<-sort(poids2)
#2. Calculer les probabilités empiriques cumulées des valeurs de x
Cumul<-c(1:length(poids2))
S<-Cumul/length(poids2)
#3. Centrer et réduire les valeurs de x
z<-(x-mean(poids2))/sd(poids2)
#4. Calculer les probabilités théoriques des valeurs de x
F<-pnorm(z,0,1)
#5. Calculer la différence entre les probabilités théoriques et empiriques
Diff1<-abs(S-F)
Diff2<-c(F[1], rep(0,length(poids2)-1))
for (i in 2:length(poids2)){
Diff2[i]<-abs(S[i-1]-F[i])
}
d<-data.frame(x,Cumul,S,z,F, Diff1,Diff2)
d## x Cumul S z F Diff1 Diff2
## 1 9.459757 1 0.03333333 -2.08462974 0.01855146 0.014781872 0.018551461
## 2 9.613224 2 0.06666667 -1.99503334 0.02301962 0.043647045 0.010313711
## 3 9.756483 3 0.10000000 -1.91139666 0.02797681 0.072023187 0.038689854
## 4 9.937877 4 0.13333333 -1.80549634 0.03549852 0.097834810 0.064501476
## 5 10.851924 5 0.16666667 -1.27186369 0.10171078 0.064955890 0.031622556
## 6 11.194571 6 0.20000000 -1.07182146 0.14190012 0.058099884 0.024766551
## 7 11.582494 7 0.23333333 -0.84534669 0.19895865 0.034374684 0.001041351
## 8 11.884506 8 0.26666667 -0.66902846 0.25173866 0.014928006 0.018405328
## 9 12.035321 9 0.30000000 -0.58098021 0.28062690 0.019373103 0.013960230
## 10 12.923106 10 0.33333333 -0.06267958 0.47501083 0.141677495 0.175010829
## 11 13.158117 11 0.36666667 0.07452329 0.52970299 0.163036327 0.196369660
## 12 13.218739 12 0.40000000 0.10991524 0.54376170 0.143761701 0.177095035
## 13 13.325800 13 0.43333333 0.17241887 0.56844588 0.135112547 0.168445880
## 14 13.408088 14 0.46666667 0.22045927 0.58724326 0.120576589 0.153909922
## 15 13.599411 15 0.50000000 0.33215622 0.63011435 0.130114350 0.163447683
## 16 13.894222 16 0.53333333 0.50427095 0.69296451 0.159631174 0.192964507
## 17 13.931306 17 0.56666667 0.52592135 0.70052857 0.133861905 0.167195238
## 18 13.934829 18 0.60000000 0.52797812 0.70124274 0.101242738 0.134576071
## 19 13.988283 19 0.63333333 0.55918547 0.71198242 0.078649091 0.111982424
## 20 14.038395 20 0.66666667 0.58844149 0.72188200 0.055215335 0.088548668
## 21 14.116704 21 0.70000000 0.63415910 0.73701150 0.037011503 0.070344836
## 22 14.160016 22 0.73333333 0.65944538 0.74519510 0.011861763 0.045195096
## 23 14.249056 23 0.76666667 0.71142775 0.76159040 0.005076271 0.028257062
## 24 14.348161 24 0.80000000 0.76928685 0.77913848 0.020861520 0.012471814
## 25 14.451904 25 0.83333333 0.82985342 0.79668917 0.036644165 0.003310831
## 26 14.565139 26 0.86666667 0.89596152 0.81486334 0.051803324 0.018469991
## 27 14.672971 27 0.90000000 0.95891504 0.83119923 0.068800773 0.035467439
## 28 14.783578 28 0.93333333 1.02348940 0.84696175 0.086371587 0.053038254
## 29 14.868687 29 0.96666667 1.07317674 0.85840409 0.108262578 0.074929245
## 30 14.961377 30 1.00000000 1.12729071 0.87019021 0.129809794 0.096476461
D1<-sort(Diff1)
D2<-sort(Diff2)
Dmax<-c(D1[length(D1)],D2[length(D2)])
Dmax## [1] 0.1630363 0.1963697Selon la table 3 ci-dessus, la valeur de D0.05 = 0.240 (pour n = 30). Etant donné que Dmaxobs (0.1963697) < D0.05 (0.240), l'H0 est tolérée.
Voici la représentation graphique du calcul de Dmax:
#Graphique
x2<-0
if (Dmax[1]>Dmax[2]){
for (i in 1:length(poids2)){
if (Diff1[i]==Dmax[1]) {
x2<-x[i]
}
}}
if (Dmax[1]<Dmax[2]){
for (i in 1:length(poids2)){
if (Diff2[i]==Dmax[2]) {
x2<-x[i]
}
}}
x2 #valeur de x de la plus grande différence entre les distributions théorique et empirique## [1] 13.15812plot(d$x,d$S, type="l", main="Poids2")
lines(d$x,d$F,col="red")
abline(v=x2, col="blue")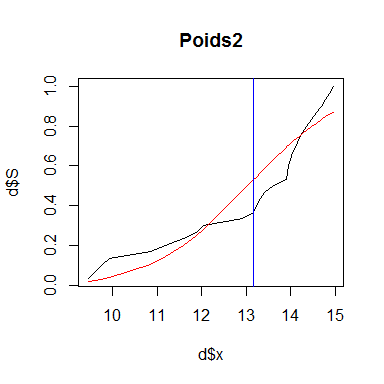
La courbe noire est la distribution cumulée observée tandis que la courbe rouge est la distribution cumulée théorique. La ligne bleue indique Dmax, c'est-à-dire l'endroit où l'écart entre les données observées et théoriques est le plus important.
Dans ce cas-ci également, il existe dans R une commande pour tester l'ajustement de données à une loi normale via le test de Kolmogorov-Smirnov: ks.test(x,"pnorm",moyenne,ecart-type)
Voici ce que cela donne avec nos deux exemples:
ks.test(poids1,"pnorm",mean(poids1),sd(poids1))##
## One-sample Kolmogorov-Smirnov test
##
## data: poids1
## D = 0.10175, p-value = 0.8845
## alternative hypothesis: two-sidedks.test(poids2,"pnorm",mean(poids2),sd(poids2))##
## One-sample Kolmogorov-Smirnov test
##
## data: poids2
## D = 0.19637, p-value = 0.1728
## alternative hypothesis: two-sidedComme on peut le constater, les valeurs de D correspondent effectivement aux valeurs de D calculées manuellement. De plus, dans les deux cas, la probabilité de dépassement est supérieure à 0.05. Cela indique que l'hypothèse de normalité des données est tolérée. Cela est assez inattendu. Mais, rappelez-vous, le test de Kolmogorov-Smirnov est surtout sensible pour de grands échantillons. Pour des échantillons plus petit, le test de Shapiro-Wilk est le plus adapté.
Voici donc deux nouveaux exemples de l'utilisation du test de Kolmogorov-Smirnov avec des échantillons beaucoup plus importants (n = 2000):
Exemple 3
#Exemple 3
poids1<-rnorm(2000,10,2)
#1. Trier les données par ordre croissant
x<-sort(poids1)
#2. Calculer les probabilités empiriques cumulées des valeurs de x
Cumul<-c(1:length(poids1))
S<-Cumul/length(poids1)
#3. Centrer et réduire les valeurs de x
z<-(x-mean(poids1))/sd(poids1)
#4. Calculer les probabilités théoriques des valeurs de x
F<-pnorm(z,0,1)
#5. Calculer la différence entre les probabilités théoriques et empiriques
Diff1<-abs(S-F)
Diff2<-c(F[1], rep(0,length(poids1)-1))
for (i in 2:length(poids1)){
Diff2[i]<-abs(S[i-1]-F[i])
}
d<-data.frame(x,Cumul,S,z,F, Diff1,Diff2)
head(d)## x Cumul S z F Diff1 Diff2
## 1 3.817911 1 0.0005 -3.034062 0.001206426 0.0007064257 0.001206426
## 2 4.025641 2 0.0010 -2.931286 0.001687810 0.0006878101 0.001187810
## 3 4.405763 3 0.0015 -2.743218 0.003042018 0.0015420181 0.002042018
## 4 4.483752 4 0.0020 -2.704632 0.003419007 0.0014190068 0.001919007
## 5 4.588411 5 0.0025 -2.652851 0.003990758 0.0014907578 0.001990758
## 6 4.613472 6 0.0030 -2.640452 0.004139779 0.0011397786 0.001639779D1<-sort(Diff1)
D2<-sort(Diff2)
Dmax<-c(D1[length(D1)],D2[length(D2)])
Dmax## [1] 0.01340368 0.01390368Selon la table 3 ci-dessus, la valeur de D0.05 = 1.36/√2000 = 0.0304 (pour n = 2000). Etant donné que Dmaxobs (0.01390368) < D0.05 (0.0304), l'H0 est tolérée.
Voici la représentation graphique du calcul de Dmax:
#Graphique
x2<-0
if (Dmax[1]>Dmax[2]){
for (i in 1:length(poids1)){
if (Diff1[i]==Dmax[1]) {
x2<-x[i]
}
}}
if (Dmax[1]<Dmax[2]){
for (i in 1:length(poids1)){
if (Diff2[i]==Dmax[2]) {
x2<-x[i]
}
}}
x2 #valeur de x de la plus grande différence entre les distributions théorique et empirique## [1] 9.069008plot(d$x,d$S, type="l", main="Poids1")
lines(d$x,d$F,col="red")
abline(v=x2, col="blue")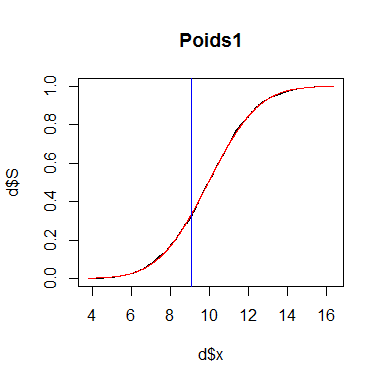
La courbe noire est la distribution cumulée observée tandis que la courbe rouge est la distribution cumulée théorique. La ligne bleue indique Dmax, c'est-à-dire l'endroit où l'écart entre les données observées et théoriques est le plus important.
Comme on peut le constater, avec la commande directe de R, nous obtenons les mêmes résultats:
ks.test(poids1,"pnorm",mean(poids1),sd(poids1))##
## One-sample Kolmogorov-Smirnov test
##
## data: poids1
## D = 0.10175, p-value = 0.8845
## alternative hypothesis: two-sidedExemple 4
#Exemple 4
poids2<-c(runif(500,8,13),runif(1500,13,15))
#1. Trier les données par ordre croissant
x<-sort(poids2)
#2. Calculer les probabilités empiriques cumulées des valeurs de x
Cumul<-c(1:length(poids2))
S<-Cumul/length(poids2)
#3. Centrer et réduire les valeurs de x
z<-(x-mean(poids2))/sd(poids2)
#4. Calculer les probabilités théoriques des valeurs de x
F<-pnorm(z,0,1)
#5. Calculer la différence entre les probabilités théoriques et empiriques
Diff1<-abs(S-F)
Diff2<-c(F[1], rep(0,length(poids2)-1))
for (i in 2:length(poids2)){
Diff2[i]<-abs(S[i-1]-F[i])
}
d<-data.frame(x,Cumul,S,z,F, Diff1,Diff2)
head(d)## x Cumul S z F Diff1 Diff2
## 1 8.006549 1 0.0005 -2.983871 0.001423135 9.231351e-04 1.423135e-03
## 2 8.020807 2 0.0010 -2.975594 0.001462109 4.621087e-04 9.621087e-04
## 3 8.029422 3 0.0015 -2.970593 0.001486126 1.387403e-05 4.861260e-04
## 4 8.038924 4 0.0020 -2.965077 0.001513035 4.869652e-04 1.303483e-05
## 5 8.042616 5 0.0025 -2.962934 0.001523609 9.763906e-04 4.763906e-04
## 6 8.049141 6 0.0030 -2.959146 0.001542463 1.457537e-03 9.575368e-04D1<-sort(Diff1)
D2<-sort(Diff2)
Dmax<-c(D1[length(D1)],D2[length(D2)])
Dmax## [1] 0.2163459 0.2168459Selon la table 3 ci-dessus, la valeur de D0.05 = 1.36/√2000 = 0.0304 (pour n = 2000). Etant donné que Dmaxobs (0.2168459) > D0.05 (0.0304), l'H0 est rejetée.
Voici la représentation graphique du calcul de Dmax:
#Graphique
x2<-0
if (Dmax[1]>Dmax[2]){
for (i in 1:length(poids2)){
if (Diff1[i]==Dmax[1]) {
x2<-x[i]
}
}}
if (Dmax[1]<Dmax[2]){
for (i in 1:length(poids2)){
if (Diff2[i]==Dmax[2]) {
x2<-x[i]
}
}}
x2 #valeur de x de la plus grande différence entre les distributions théorique et empirique## [1] 13.00555plot(d$x,d$S, type="l", main="Poids2")
lines(d$x,d$F,col="red")
abline(v=x2, col="blue")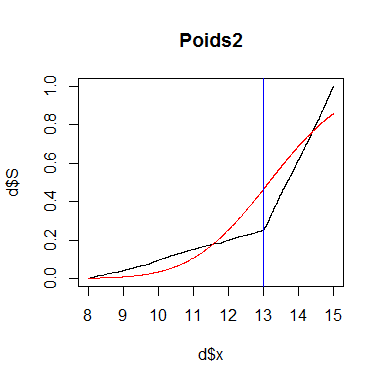
La courbe noire est la distribution cumulée observée tandis que la courbe rouge est la distribution cumulée théorique. La ligne bleue indique Dmax, c'est-à-dire l'endroit où l'écart entre les données observées et théoriques est le plus important.
Comme on peut le constater, avec la commande directe de R, nous obtenons les mêmes résultats:
ks.test(poids2,"pnorm",mean(poids2),sd(poids2))##
## One-sample Kolmogorov-Smirnov test
##
## data: poids2
## D = 0.21173, p-value < 2.2e-16
## alternative hypothesis: two-sided