Exemple d'examen de R
Voici une autre illustration: il s'agit des questions de l'examen de travaux pratiques de septembre 2012.
I. Puissance d'un test de comparaison de deux échantillons en fonction de l'écart entre les populations
Il est clair que, dans les situations où on souhaite tester si deux échantillons proviennent de deux populations normales de même moyenne et de même variance, la puissance du test de détection dépendra de l'écart entre les deux populations. Si l'écart est nul (c'est-à-dire, si l'hypothèse nulle H0: μ1=μ2 est vraie), le test ne devrait idéalement détecter aucune différence. Malheureusement, les tests n'étant pas parfaits, le test commettra des erreurs de type I, et donc déclarera erronnément la différence observée entre les échantillons comme étant significative dans une proportion de cas approximativement égale à α. Si, par contre, l'écart entre les deux moyennes des distributions n'est pas nul (μ1 ≠ μ2), le test déclarera à juste titre qu'il y a une différence entre les distributions dans une proportion de cas qui correspond à la puissance et qui vaut P=1-β. Bien entendu, plus l'écart sera important et plus la puissance augmentera. Attention que l'écart entre les moyennes est un écart relatif: un même écart pourrait être significatif si les données varient beaucoup (σ >>), et ne pas l'être si elles varient peu (σ <<). Pour cette raison, on exprimera l'écart en "nombre d de déviations standards", ce qui revient à écrire que: d = |μ1-μ2|/σ. Ces précisions étant apportées, voici l'énoncé du problème de l'examen de septembre 2012:
Les tests de comparaisons de deux groupes ont une puissance qui dépend d'une part de l'effectif des groupes (n1, n2), et d'autre part de la différence moyenne standardisée entre les groupes (d = |μ1-μ2|/σ). Afin de mettre en évidence la relation entre puissance (au seuil α = 0.05) et différence moyenne standardisée, nous allons effectuer la simulation suivante en gardant les effectifs constants (par exemple, n1=n2=10). On va faire varier d de 0.0 à 2.0 par pas de 0.1 (remarque : μ2 = μ1 + σ*d), et, pour chaque situation, simuler 1000 fois les 2 échantillons, calculer la statistique correspondant au test de l'hypothèse nulle H0: μ1=μ2, et comptabiliser la proportion de situations où le test détecte une différence.
Le code est donc le suivant:
n1<-10
n2<-10
mu1<-0
sigma<-1
power<-vector(length=11)
dlist<-seq(0.0,2.0,0.1)
i<-0
for (d in dlist) {
i<-i+1
c<-0
mu2<-mu1+sigma*d
for (r in 1:1000){
s1<-rnorm(n1,mu1,sigma)
s2<-rnorm(n2,mu2,sigma)
t<-t.test(s1,s2,var.equal=TRUE)
if (t$p.value<0.05) {c<-c+1}
}
power[i]<-1.0*c/1000
}
plot(dlist,power,type="l")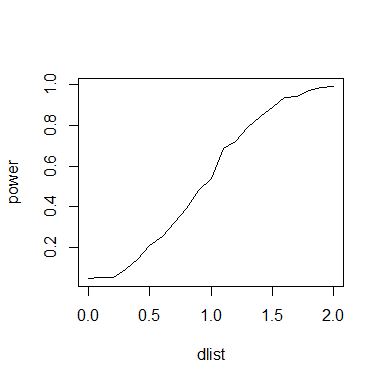
- Les lignes 1 et 2 servent à initialiser les variables n1 et n2, qui sont les tailles d'échantillons utilisées.
- La ligne 3 initialise arbitrairement à 0 la moyenne de la population (normale) dont proviendront les échantillons 1. La valeur de cette moyenne est quelconque, étant entendu que seule la différence standardisée entre les moyennes influe sur la puissance.
- La ligne 4 choisit arbitrairement la valeur de la déviation standard des deux populations utilisées. Voir remarque au point précédent.
- Comme on aura 11 valeurs de d à tester, on va obtenir 11 puissances. La ligne 5 définit le vecteur destiné à contenir ces 11 nombres.
- La ligne 6 permet de générer les 11 valeurs de d à utiliser.
- i est un compteur qui sera incrémenté chaque fois que la valeur de d changera. Pour la première valeur de d, i vaudra 1 et la puissance obtenue sera placée dans le vecteur des résultats en power[i]=power[1]. La seconde valeur de d verra i valoir d, et le résultat correspondant ser placé dans power[i]=power[2], etc...
- La ligne 8 permet d'entamer la boucle sur les valeurs de d. Cett boucle se termine en ligne 19.
- Comme dit plus haut, le compteur i est incrémenté à chaque changement de valeur de d
- c est un compteur utilisé pour comptabiliser le nombre de fois où, dans les 1000 simulations qui vont suivre, le test effectué sera significatif. Initialement, le compteur est mis à 0.
- Une fois les valeurs de d et de σ fixées, la valeur de μ2 est également fixée: μ2 = μ1 + σ*d.
- La ligne 12 entame la boucle sur les 1000 répétitions. Cette boucle se termine en ligne 17.
- Les lignes 13 et 14 tirent aléatoirement des échantillons de tailles respectives n1 et n2 dans des distributions normales de moyennes respectives μ1 et μ2 et de déviation standard commune σ. Ces deux échantillons sont placés respectivement dans s1 et s2.
- La ligne 15 permet de réaliser un test de t pour échantillons supposés provenir de populations (normales) de mêmes variances (VAR.EQUAL=TRUE). Le résultat du test est placé dans la variable t.
- La seule caractéristique du test qui nous importe dans l'exercice est la valeur p associée au test: si cette valeur p est inférieure à 0.05, cela signifie que le test est significatif, et donc que le compteur c doit être incrémenté. C'est l'objet de la ligne 16.
- La ligne 18 calcule la puissance associée au d en cours. Il s'agit du rapport entre le nombre de simulations ayant donné un résultat significatif et le nombre total de simulations (1000). Ce rapport est donc placé dans le vecteur power pour être affiché plus tard.
- La ligne 20 ne sera atteinte qu'une fois que toutes les valeurs successives de d auront été parcourues et que le vecteur power aura donc été rempli. Cette dernière instruction permet de faire un graphique de la puissance en fonction de la valeur de d, et ainsi montrer que la puissance évolue de manière sigmoide de P=0.05 quand d=0 vers P=1.00 quand d devient grand.
II. Puissance d'un test de comparaison de deux échantillons en fonction de la taille des échantillons
Le raisonnement est similaire à celui de la question précédente: on garde cette fois la différence standardisée entre les moyennes constante (arbitrairement, on a choisi μ2 = μ1 + σ*1.0, ce qui revient à prendre une valeur de d = 1.0 dans l'exemple précédent. Il est clair que si on choisit une autre valeur de d, les puissances obtenues vont différer de celles présentées ici). On fait cette fois varier les tailles d'échantillons (on choisit toutefois de garder n1=n2. On pourrait évidemment imaginer de faire les calculs pour des valeurs différentes des deux effectifs). Le programme est similaire au programme de la question 1:
d<-1.0
sigma<-1
mu1<-0
mu2<-mu1+d*sigma
power<-vector(length=10)
nlist<-seq(2,20,2)
i<-0
for (n in nlist){
i<-i+1
c<-0
for (r in 1:1000){
s1<-rnorm(n,mu1,sigma)
s2<-rnorm(n,mu2,sigma)
t<-t.test(s1,s2,var.equal=TRUE)
if(t$p.value<0.05) {c<-c+1}
}
power[i]<-1.0*c/1000
}
plot(nlist,power,type="l")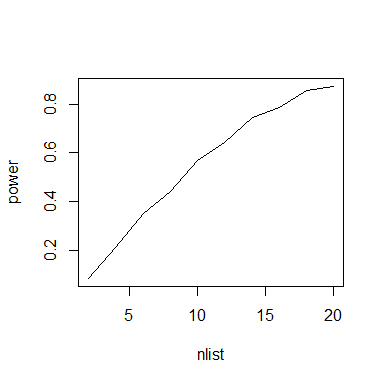
Le code est très similaire à celui de la question 1. La boucle externe est cette fois sur les tailles d'échantillons (n), et la boucle interne reste la boucle sur les simulations (r).