Test t de student : Deux échantillons indépendants

Le test t de student permet de tester si les moyennes de deux groupes diffèrent ou non entre elles. En d'autres mots, on cherche à savoir si une variable indépendante discrète composée de deux modalités (groupes) a un effet sur une variable dépendante continue. Les hypothèses à tester sont donc:

H0: Les moyennes des deux groupes sont identiques: μ₁ = μ₂
HA: Les moyennes des deux groupes sont différentes: μ₁ ≠ μ₂

Pour illustrer cela, nous allons prendre l'exemple suivant : imaginons 20 veaux répartis en deux groupes : 10 dont les mères ont reçu un traitement pendant la gestation (MT) et 10 dont les mères n'ont pas reçu de traitement durant la gestation (MNT). On mesure le poids des veaux à la naissance et on veut savoir si les poids des veaux dont les mères ont été traitées sont significativement inférieurs à ceux dont les mères n'ont pas été traitées. Notez que nous sommes dans un test unilatéral. L'hypothèse alternative dans ce cas-ci est μ_MT < μ_MNT.

Voici les données obtenues:

MT	32.9	35.1	37.5	29.6	21.6	31.4	26.6	26.0	31.4	28.2
MNT	35.3	41.9	32.9	34.7	37.4	38.4	41.3	29.9	33.4	40.9

Avant de réaliser le test t de student, il faut vérifier que les variances des deux groupes sont statistiquement égales. L'égalité des variances peut se tester grace au test F et à la fonction var.test(echantillon1,echantillon2). Dans notre exemple, cela donne:

MT<-c(32.9,35.1,37.5,29.6,21.6,31.4,26.6,26.0,31.4,28.2)
MNT<-c(35.3,41.9,32.9,34.7,37.4,38.4,41.3,29.9,33.4,40.9)
var.test(MT,MNT)

## 
##  F test to compare two variances
## 
## data:  MT and MNT
## F = 1.337, num df = 9, denom df = 9, p-value = 0.6723
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.3320996 5.3828790
## sample estimates:
## ratio of variances 
##           1.337031

On obtient une valeur de F de 1.337 et une probabilité associée à cette valeur de 0.6723. Etant donné que cette probabilité de dépassement (p-value) est supérieure à 0.05, nous pouvons tolérer l'hypothèse nulle d'égalité des variances.

Maintenant que nous savons que les deux variances sont statistiquement égales, nous pouvons comparer les deux échantillons de veaux en partant de l'hypothèse nulle que ces deux échantillons proviennent tous les deux de la même population, supposée normale. En d'autres mots, on supposera donc que les estimateurs de variance qu'on pourrait calculer avec chaque échantillon estiment en réalité la même variance (celle de la population d'origine des échantillons), et que, si l'hypothèse nulle est vraie, les estimateurs de moyennes estiment la même variance. Dans ces conditions, on peut tester aisément l'hypothèse nulle à partir de la statistique t.

Pour rappel, voici la formule pour calculer t à partir de deux échantillons indépendants et de variances égales:

\[ t = \frac{(\bar{X_1}-\bar{X_2})-(\mu_1 -\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\]

Dans R, de manière explicite, cela donne:

moyMT<-mean(MT)
moyMNT<-mean(MNT)
varMT<-var(MT)
varMNT<-var(MNT)
nMT<-10
nMNT<-10
t<-(moyMT-moyMNT)/sqrt(varMT/nMT + varMNT/nMNT)
t

## [1] -3.371675

dl<-nMT+nMNT-2
pt(t,dl)

## [1] 0.001699018

On obtient une valeur de t égale à -3.37. La probabilité d'obtenir une valeur aussi faible si l'H0 est vraie (c'est-à-dire si les moyennes dans les populations sont égales) est de 0.0017. Etant donné que cette probabilité est très faible (< 0.05), on peut rejeter l'H0 et conclure que le poids des veaux des mères traitées est significativement inférieur au poids des veaux des mères non traitées.

On peut obtenir ce même résultat de manière implicite en utilisant la fonction t.test(<arguments>).

t.test(MT,MNT, alternative="less", var.equal=TRUE)

## 
##  Two Sample t-test
## 
## data:  MT and MNT
## t = -3.3717, df = 18, p-value = 0.001699
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##       -Inf -3.195885
## sample estimates:
## mean of x mean of y 
##     30.03     36.61

Comme attendu, on obtient exactement le même résultat:

la valeur de t qui est de -3.3717
le nombre de degré de liberté: 18
la probabilité d'obtenir une valeur de t aussi petite: p= 0.001699
les moyennes de nos deux échantillons: 30.03 et 36.61

Remarquez qu'il faut préciser que les deux variances des populations d'origine des échantillons sont supposées égales via l'option var.equal=TRUE parce que R considère par défaut que les deux variances sont différentes et adapte le test en conséquence (le nombre de degrés de liberté notamment est adapté en utilisant une approximation de Welch ou de Satterthwaite, mais ce cas dépasse le cadre du cours d'introduction).

Une syntaxe alternative

Signalons qu'il existe une autre syntaxe de la fonction t.test. Cette syntaxe est surtout utile lorsque les données à analyser sont dans un format dans lequel chaque ligne correspond à une observation, avec une colonne qui donne les valeurs à comparer et une autre qui donne le groupe auquel la valeur correspondante appartient. Ce format est très souvent utilisé lorsqu'on travaille avec des fichiers de données externes, et nous allons l'utiliser pour ce cas de figure. Supposons donc que les données du test des deux échantillons de poids données plus haut proviennent d'un fichier externe. Ce fichier se présenterait par exemple de la manière suivante:

Figure 1: Le fichier de données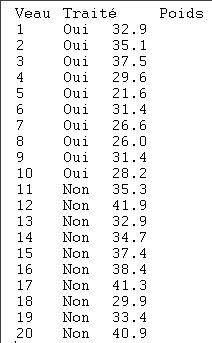

Après avoir lu ce fichier, on dispose donc des 20 données dans la première colonne, et de leur groupe via la seconde colonne. Une variable telle que celle créée pour représenter les "valeurs" de la seconde colonne est appelée un facteur. On pourrait évidemment retravailler ces deux variables pour se ramener au cas décrit plus haut, mais on peut utiliser directement la syntaxe alternative de la commande t.test, qui prend la forme suivante: t.test(valeur ~ facteur, <autres arguments>). L'écriture valeur ~ facteur est un raccourci pour dire que la valeur à gauche du ~ est la variable dépendante, et à droite figure(nt) la(les) variable(s) ou facteur(s) indépendant(s). Dans le cas simple qui nous occupe ici, on peut donc écrire:

veau<-c(1:20)
traité<-c(rep("Oui",10),rep("Non",10))
poids<-c(MT,MNT)
d<-data.frame(veau,traité,poids)
d

##    veau traité poids
## 1     1    Oui  32.9
## 2     2    Oui  35.1
## 3     3    Oui  37.5
## 4     4    Oui  29.6
## 5     5    Oui  21.6
## 6     6    Oui  31.4
## 7     7    Oui  26.6
## 8     8    Oui  26.0
## 9     9    Oui  31.4
## 10   10    Oui  28.2
## 11   11    Non  35.3
## 12   12    Non  41.9
## 13   13    Non  32.9
## 14   14    Non  34.7
## 15   15    Non  37.4
## 16   16    Non  38.4
## 17   17    Non  41.3
## 18   18    Non  29.9
## 19   19    Non  33.4
## 20   20    Non  40.9

t.test(d$poids~d$traité, var.equal=TRUE, alternative="greater")

## 
##  Two Sample t-test
## 
## data:  d$poids by d$traité
## t = 3.3717, df = 18, p-value = 0.001699
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  3.195885      Inf
## sample estimates:
## mean in group Non mean in group Oui 
##             36.61             30.03

Notez que cette fois-ci, on a précisé comme hypothèse alternative "greater" et non "less" comme précédemment. Cela est dû à l'ordre dans lequel les données sont présentées. Précédemment, on avait regardé la différence entre MT et MNT. Etant donné que notre hypothèse alternative est que la moyenne du groupe MT est inférieure à celle du groupe MNT, on regarde si la différence entre MT et MNT est inférieure à 0. C'est pourquoi, on précise alternative="less". C'est d'ailleurs pour cette raison que la valeur de t est négative et que l'on regarde la probabilité d'avoir une valeur de t aussi faible.
Par contre, dans le dernier cas, R fait la différence entre MNT et MT. Dès lors, dans ce cas-ci, on regarde si la différence entre MNT et MT est supérieure à 0. C'est pourquoi, on précise alternative="greater". Et dans ce cas-ci, la valeur de t est positive et on regarde la probabilité d'avoir une valeur de t aussi élevée.

Pour connaître l'ordre des moyennes utilisé par R et choisir la bonne hypothèse alternative, on peut demander à R de nous spécifier les niveaux de la variable facteur:

levels(d$traité)

## [1] "Non" "Oui"

R fera toujours la différence entre le premier et le deuxième niveau. Donc, dans ce cas-ci, il fait la différence entre le poids des veaux provenant de mères non traitées et celui des veaux provenant de mères traitées.

De manière explicite, cela correspond à :

moyMT<-mean(MT)
moyMNT<-mean(MNT)
varMT<-var(MT)
varMNT<-var(MNT)
nMT<-10
nMNT<-10
t<-(moyMNT-moyMT)/sqrt(varMT/nMT + varMNT/nMNT)
t

## [1] 3.371675

dl<-nMT+nMNT-2
1-pt(t,dl)

## [1] 0.001699018