Les statistiques inférentielles
I. Démarche du test d'hypothèse
Dans les statistiques inférentielles, il ne s'agit plus simplement de calculer des paramètres sur un échantillon, mais de tester si les mesures prises sur cet échantillon peuvent être généralisées à l'entiéreté de la population dont il provient.
Le déroulement d'un test d'hypothèse suit toujours le même shéma :
- Poser les hypothèses :
- Effectuer les calculs permettant d'arriver à un paramètre statistique
- Analyser la probabilité du résultat obtenu
- Décider de rejetter ou non H0:
H0 (hypothèse nulle) : aucun effet au niveau de la population
H1 (hypothèse alternative) : effet au niveau de la population
Lorsque le paramètre statistique obtenu dépasse une valeur critique, ce qui revient à ce que la probabilité de ce paramètre soit inférieur à un seuil critique (fixé, par défaut, à p=0.05), l'hypothèse nulle est rejetée et on conclut alors à un effet significatif au niveau de la population. Au contraire, lorsque le paramètre statistique reste en dessous d'une valeur critique, et donc que sa probabilité est supérieure au seuil critique, l'hypothèse nulle est tolérée et il n'est alors pas possible de conclure à un effet significatif au niveau de la population.
Illustrons cette décision à l'aide de grahiques.
Le graphique ci-dessous représente la distribution de Z. La valeur critique de Z pour un test unilatéral droit dans la table équivaut à 1.64 comme cela est indiqué en rouge sur ce graphique. La probabilité d'avoir une valeur supérieure à 1.64 est égale à 0.05 comme cela est indiqué en bleu sur le graphique. A partir de ce graphique, on peut donc comprendre que si on a une valeur de Z supérieure à 1.64, cela signifie que la probabilité associée à cette valeur est inférieure à 0.05 et donc que l'on rejette H0. Inversement, si on a une valeur de Z inférieure à 1.64, la probabilité associée à cette valeur sera supérieure à 0.05 et donc on acceptera H0.
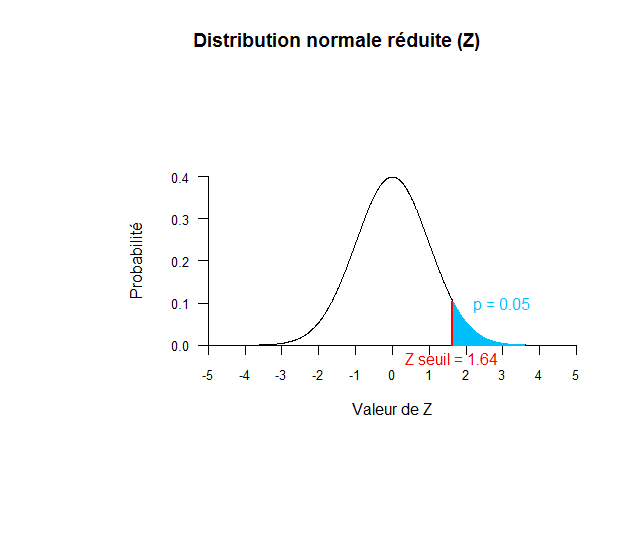
Le graphique suivant illustre la même démarche mais lorsqu'on se trouve dans une distribution de chi-carré à 3 degrés de liberté. La valeur critique de chi-carré avec 3 degrés de liberté équivaut à 7.81 comme cela est indiqué en rouge sur ce graphique. La probabilité d'avoir une valeur supérieure à 7.81 est égale à 0.05 comme cela est indiqué en bleu sur le graphique. A partir de ce graphique, on peut donc comprendre que si on a une valeur de chi-carré supérieure à 7.81, cela signifie que la probabilité associée à cette valeur est inférieure à 0.05 et donc que l'on rejette H0. Inversement, si on a une valeur de chi-carré inférieure à 7.81, la probabilité associée à cette valeur sera supérieure à 0.05 et donc on acceptera H0.
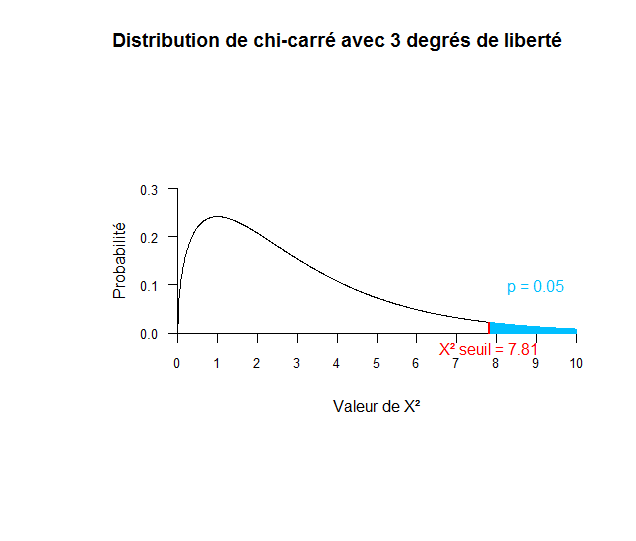
Avec ces deux graphiques, on comprend bien que comparer la statistique observée à une statistique seuil équivaut à comparer la probabilité observée à la probabilité seuil de 0.05.
Les statistiques seuil se trouvent dans les tables des distributions mais elles peuvent également se trouver facilement dans R avec la fonction q suivi du nom de la distribution.
qnorm(0.95) #Distribution de Z## [1] 1.644854qchisq(0.95,3) #Distribution de chi-carré avec 3 degrés de liberté## [1] 7.814728qt(0.95,2) #Distribution de t avec 2 degrés de liberté## [1] 2.919986qf(0.95,2,4) #Distribution de F avec 2 et 4 degrés de liberté## [1] 6.944272II. Choix du test inférentiel
Le tableau ci-dessous reprend les principaux tests de statistique inférentielle de base. Le choix du test à utiliser est fonction du type de données récoltées, de leurs propriétés et des effets à tester. Dans les grandes lignes, on peut vouloir tester si des variables ont un lien entre elles ou si certaines variables (VI = variable indépendante) en influencent d'autres (VD = variable dépendante). En cliquant sur le nom de chaque test, vous accéderez à des explications détaillées le concernant.