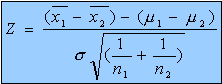- On considère que le poids des chiots bergers allemands à la naissance suit une distribution normale, de moyenne 0,150 kg et de variance 0,015. On suspecte cependant que les chiennes diabétiques mettent au monde des chiots qui ont en moyenne un poids inférieur à 0,150 kg. Afin de vérifier cette hypothèse, on a relevé le poids de 25 chiots bergers allemands nés de mères diabétiques et le poids moyen observé a été de 0,2 kg. On demande:
a) quelle est la probabilité d'observer un poids moyen aussi élevé ou plus élevé si les chiots nés de mères diabétiques obéissent à la loi générale?
b) quelle hypothèse acceptera-t-on?
- Dans un élevage de souris, la taille des portées est en moyenne de 10 jeunes, avec déviation standard de 2,5. Combien faut-il produire de nichées pour avoir 97,5 chances sur 100 de produire au moins 50 jeunes? On admet que la taille des portées est distribuée normalement.
- Un régime particulier, chez des bovins, augmente le poids en moyenne de 20 kgs a un âge donné. Chez les bovins n'ayant pas subi le régime , le poids à cet âge est N(700;50^2). Un expérimentateur désire vérifier ce gain dans sa population et fait une expérience sur 20 bêtes qu'il soumet au régime. Calculez la puissance de l'expérience de manière théorique et empirique.
- Deux populations bactériennes ont une sensibilité différente à la pénicilline. La première est caractérisée par un diamètre moyen de la zone d'inhibition de la croissance de 11 mm, avec une déviation standard de 1 mm (la distribution est supposée normale). La seconde a un diamètre moyen de 8 mm, avec une déviation standard de 0,8 mm. On désire déterminer la population d'origine d'une colonie en examinant la taille d'une plage. On demande:
a) de calculer les valeurs seuils menant à une erreur de type 1 de 5 % et 1 %.
b) pour chacune de ces valeurs seuils, donnez l'erreur de type 2 ainsi que la puissance du test.
- On a comparé le taux sanguin de créatine chez des veaux culards et chez des veaux non culards :
| Culards | Non culards |
| 4,2 | 2,8 |
| 3,9 | 2,1 |
| 3,7 | 3 |
| 3,5 | 2,3 |
| 4 | 2,4 |
| 2,7 |
La différence entre les deux moyennes est-elle significative?
- On désire vérifier si deux populations données, A et B, ont même moyenne. On prélève un échantillon de taille n=50 dans la population A et un échantillon de taille n=100 dans la population B. On trouve: 35,6 de moyenne pour l'échantillon provenant de A et 34,7 pour celle de B. Quelles sont vos conclusions, sachant que la variance des 2 populations est de 3.
- Calculez la distribution du statistique S obtenu en prélevant deux échantillons de tailles respectives n1 et n2 dans deux populations normales de déviation standard "sigma" et de moyennes respectives "mu1" et "mu2" et obtenu en calculant:
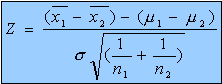
- Sur 5 individus, on a effectué une numération globulaire au mois de janvier; on a répété la même numération en avril. On a obtenu les valeurs suivantes:
| Individus | Janvier | Avril |
| A | 46 | 46 (x 100.000/mm³) |
| B | 38 | 42 |
| C | 42 | 44 |
| D | 43 | 47 |
| E | 45 | 48 |
On demande si les 5 individus ont, en moyenne, la même numération globulaire, à ces 2 moments de l'année.
- Dix chiens d'une race réputée aggressive ont été utilisés dans une expérience portant sur l'amélioration des caractères comportementaux. Ces derniers sont mesurés par une cote comprise entre 1 et 20, de moyenne 8 et de déviation standard 3, les cotes basses indiquant des chiens plus paisibles. Les chiens de l'expérience sont mis dans des conditions de relations tendant à les sociabiliser, et le résultat moyen obtenu pour cet échantillon est de 7.2. Testez l'effet de ce traitement. Donnez l'hypothèse nulle, la manière de la tester, le statistique utilisée, la zone de réjection et la conclusion du test.
- Les mesures (en mm.) faites sur l'épaisseur du lard dorsal chez 10 porcs ont donné les résultats suivants:
47, 38, 39, 32, 34, 37, 31, 43, 41, 43
Quelle est la probabilité d'obtenir de telles valeur si la valeur moyenne dans cette population est de 42 mm. ? Pour quelles valeurs moyennes ces résultats n'ont-ils que 2.5 % de chance d'arriver (si les porcs proviennent bien de cette population) ?
- On a comparé les poids en livres de deux lots de génisses Holstein. Un lot a reçu un supplément de vitamine A, l'autre a servi de témoin. Les gains moyens sont-ils significativement différents ?
Témoin: 175, 132, 218, 151, 200, 219, 234, 149, 187, 123, 248, 206, 179, 206
Vitamine A: 142, 311, 337, 262, 302, 195, 253, 199, 236, 216, 211, 176, 249, 214
- On a dosé l'hydroxyproline (un acide aminé spécifique du tissu conjonctif) dans 5 muscles, par deux méthodes différentes. Les résultats sont les suivants:
|
|
Méthode A |
Méthode B |
|
Muscle Ilio-spinal |
12 |
9 |
|
Gluteus Medius |
11 |
11 |
|
Gracilis |
13 |
10 |
|
Brachial |
8 |
7 |
|
Tr. Femoram |
8 |
9 |
La méthode A donne-t-elle des résultats significativement plus élevés que la méthode B ?
- A supposer que le taux de fécondation soit de 60%, combien de vaches faut-il inséminer pour produire au moins 30 femelles dans 95% des cas ? Donnez deux méthodes possibles pour résoudre le problème, et utilisez la méthode qui vous semble la plus simple.
- Un généticien a besoin de 50 souris d'un type génétique particulier. Dans les lignées de parents potentiels, la taille de portée est en moyenne de 10 jeunes, avec une déviation standard de 2.5. Si on admet que la taille de portée est distribuée normalement, combien faudra-t-il produire de nichées pour avoir 97.5% de chances d'obtenir ces 50 souriceaux ?
- Un expérimentateur estime qu'un régime qu'il a mis au point améliore de manière significative les performances (poids) des individus soumis à ce régime. Pour vérifier son hypothèse, il prélève (au hasard) 20 individus dans la population qui l'intéresse, caractérisée par une moyenne pondérale de 40 kilos et une déviation standard de 6 kilos. Après avoir soumis ces 20 individus au régime qu'il préconise, il les pèse et obtient une moyenne de 42 kilos. Ses espoirs sont-ils fondés ? Calculez l'erreur de type I du test. Si effectivement le traitement a pour effet d'augmenter de 2 kilos le poids des animaux, quelle est la puissance du test (au seuil α=5%) ? Quel est l'effectif à utiliser pour avoir une puissance d'au moins 90% ?
- Deux groupes de rats femelles sont soumis à des régimes de teneurs protéiques différentes, et on a mesuré, pour chaque rat, le gain pondéral (en grammes) réalisé entre les 24eme et le 84eme jours d'âge. Les résultats sont les suivants:
| teneur protéique élevée |
teneur protéique faible |
| 134 |
70 |
| 146 |
118 |
| 104 |
101 |
| 119 |
85 |
| 124 |
107 |
| 161 |
132 |
| 107 |
94 |
| 83 |
|
| 113 |
|
| 124 |
|
| 97 |
|
| 123 |
|
La différence entre les gains pondéraux est-elle significative ?
Que représente le dénominateur du statistique que vous utilisez ?
Quelle(s) hypothèse(s) avez-vous faite(s) pour utiliser ce statistique ?
- Un laboratoire de médecine humaine vient de mettre au point un nouveau produit à propriétés sédatives, et on se demande si celui-ci n'aurait pas d'effets secondaires sur la tension artérielle. Dans ce but, on constitue au hasard un groupe de 10 sujets, situés dans une décade fixée (40 à 50 ans, p. e.). Chaque individu reçoit deux préparations: un placebo une fois, et la préparation complète l'autre fois. L'expérience peut être représentée comme suit (p représente le placebo, et m le médicament):
|
Jour 1 |
Jour 2 |
|
préparation |
tension artérielle |
préparation |
tension artérielle |
| individu 1 |
p |
17 |
m |
10 |
| individu 2 |
m |
17 |
p |
15 |
| individu 3 |
p |
15 |
m |
13 |
| individu 4 |
m |
13 |
p |
13 |
| individu 5 |
p |
12 |
m |
11 |
| individu 6 |
m |
14 |
p |
17 |
| individu 7 |
p |
15 |
m |
13 |
| individu 8 |
m |
12 |
p |
19 |
| individu 9 |
p |
11 |
m |
11 |
| individu 10 |
m |
16 |
p |
16 |
Comment formulez-vous votre hypothèse nulle ? Quelle conclusion tirez-vous ? Expliquez en quoi le design expérimental permet d'éliminer certains effets de nuisance (lesquels ?).